Сравнение дисперсий двух многомерных выборочных совокупностей. Сравнение ковариационных матриц возможно с помощью критерия обобщённых дисперсий, являющегося многомерным аналогом F-критерия. Пусть имеются две группы наблюдений объёмом n₁ и n₂ . Найдём для них ковариационные матрицы [D₁] и [D₂]. Сформулируем нулевую гипотезу H₀: |D₁| = |D₂| при альтернативе H₁: |D₁| |D₂|. Объединим выборки и получим обобщённую оценку ковариационной матрицы [D], предполагаемую общей для исследуемых генеральных совокупностей. Далее вычислим статистику M:

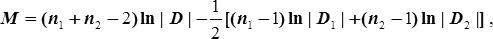           (1.3)

представляющую собой разность между логарифмом определителя обобщённой ковариационной матрицы и средним значением логарифмов определителей выборочных ковариационных матриц. Критическое значение статистики M аппроксимируется 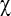-квадрат распределением с числом степеней свободы равным 0,5p(p+1), где p мерность случайной величины.

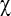²= MC^-1 ;  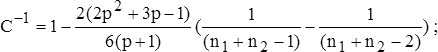          (1.4)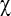

²-аппроксимация будет более точной, если количество наблюдений в каждой из выборок превышает 20.

Если полученное значение M превосходит критическое, то нулевая гипотеза о равенстве ковариационных матриц должна быть отвергнута в пользу альтернативной.