Собственные значения и собственные векторы. Исключительный практический интерес (особенно для факторного анализа) представляют собственные векторы и собственные значения квадратных матриц. Собственным значением (собственным числом, характеристическим числом) называется корень _i характеристического уравнения квадратной матрицы, которое, например, для матрицы S будет иметь вид:

Корней (собственных значений) у уравнения, которое получится, если вычислить определитель, будет столько, чему равен ранг матрицы S. Не вдаваясь в математические подробности и доказательства, приведём лишь способ использования теории собственных чисел и собственных векторов в методах многомерного прикладного анализа. Для каждого отдельного собственного числа _к находят собственный вектор, решая систему m однородных линейных уравнений вида:

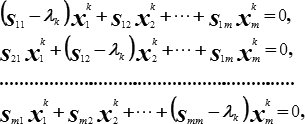
где 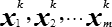- решение системы и одновременно элементы собственного вектора [Х_k]. Собственные векторы обладают одним замечательным свойством, а именно, - собственные векторы, принадлежащие различным собственным значениям, линейно независимы (ортогональны). Это свойство используется в факторном анализе. Если [S] - корреляционная матрица, то собственные векторы этой матрицы являются искомыми факторами.

В электронных таблицах каждый элемент матрицы занимает соответствующую ячейку, располагающуюся на пересечении строки и столбца. Представление этого элемента (его формат) в принципе не зависит от представления другого элемента данных. Аналогичным образом многомерные выборки организованы в таблицах прикладных статистических программ типа Statistica. С точки зрения программного кода многомерная выборка всегда представлена как массив индексированных переменных: ИМЯ (число строк, число столбцов).