Приведем описание лабораторных работ по разделам изучаемого курса «Методы оптимизации». Разделам курса в приложении mo.exe соответствуют корневые ветви дерева методов и алгоритмов.
Один из способов безусловной оптимизации, обоснованный в рамках курса математического анализа, – это использование необходимых и достаточных условий экстремума функции.
Рассмотрим функцию 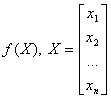 , которую нужно исследовать на максимум или минимум. Напомним некоторые определения. Частная производная функции
, которую нужно исследовать на максимум или минимум. Напомним некоторые определения. Частная производная функции 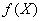 по переменной xi обозначается
по переменной xi обозначается 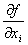 . Главная (линейная) часть приращения функции называется дифференциалом функции и обозначается df(X). По определению
. Главная (линейная) часть приращения функции называется дифференциалом функции и обозначается df(X). По определению 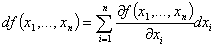 , где
, где 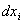 – дифференциалы (приращения) независимых переменных.
– дифференциалы (приращения) независимых переменных.
Вектор в пространстве 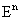 , координатами которого являются частные производные функции
, координатами которого являются частные производные функции 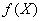 в некоторой точке X0, называется градиентом функции в данной точке и обозначается grad f(X0) или
в некоторой точке X0, называется градиентом функции в данной точке и обозначается grad f(X0) или 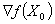 . Вектор градиента функции в точке определяет величину и направление скорости наибольшего роста функции в данной точке, т.е. представляет собой наибольшую из всех производных по направлению:
. Вектор градиента функции в точке определяет величину и направление скорости наибольшего роста функции в данной точке, т.е. представляет собой наибольшую из всех производных по направлению: 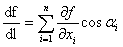 . Здесь
. Здесь 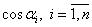 – направляющие косинусы заданного направления l..
– направляющие косинусы заданного направления l..
Напомним, что уравнение 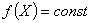 определяет поверхность уровня (поверхность постоянного значения целевой функции). Можно показать, что вектор градиента в каждой точке ортогонален соответствующей поверхности уровня.
определяет поверхность уровня (поверхность постоянного значения целевой функции). Можно показать, что вектор градиента в каждой точке ортогонален соответствующей поверхности уровня.
Особое значение при исследовании функции на экстремум имеет матрица, составленная из вторых частных производных функции 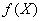 (матрица Гессе):
(матрица Гессе):
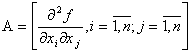 .
.С учетом введенных обозначений сформулируем необходимые и достаточные условия существования экстремума функции в точке.
Необходимые условия:
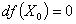 , или
, или 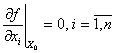 , или
, или 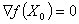 .
.Достаточные условия:
Пусть функция 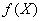 дважды непрерывно дифференцируема в окрестности
дважды непрерывно дифференцируема в окрестности 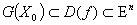 . В точке
. В точке 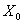 выполнены необходимые условия. Если, кроме того, положительно (отрицательно) определена квадратичная форма
выполнены необходимые условия. Если, кроме того, положительно (отрицательно) определена квадратичная форма
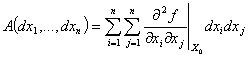 ,
,то функция 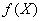 в точке
в точке 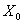 имеет минимум (максимум).
имеет минимум (максимум).
Если квадратичная форма является знакопеременной, то экстремума нет. Если квадратичная форма равна нулю, то требуются дополнительные исследования. Знаковая определенность квадратичной формы обычно исследуется по критерию Сильвестра. Для этого рассматриваются главные миноры матрицы Гессе. Если
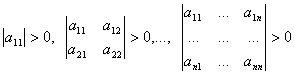 ,
,то квадратичная форма положительно определена. Если
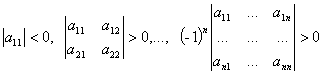 ,
,то отрицательно определена. В остальных случаях знаковая определенность отсутствует.
Необходимые условия представляют собой систему уравнений, решение которой является самостоятельной, в общем случае достаточно трудоемкой задачей. Исследование главных миноров на знак также является, как правило, нетривиальной проблемой. Поэтому широкое развитие получили различные приближенные процедуры поиска экстремумов.
Будем искать минимум целевой функции 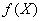 . Пусть удалось построить последовательность точек
. Пусть удалось построить последовательность точек 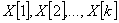 такую, что
такую, что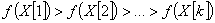 . Можно надеяться, что при
. Можно надеяться, что при 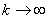 удастся найти точку минимума, соответствующим образом выбрав условие останова. Способы построения таких последовательностей называются методами спуска. Если при построении релаксационной последовательности используются вторые производные целевой функции, то метод спуска называется методом второго порядка, при использовании только первых производных имеем метод первого порядка. Если в процессе минимизации вычисление производных не производится, речь идет о поисковых методах.
удастся найти точку минимума, соответствующим образом выбрав условие останова. Способы построения таких последовательностей называются методами спуска. Если при построении релаксационной последовательности используются вторые производные целевой функции, то метод спуска называется методом второго порядка, при использовании только первых производных имеем метод первого порядка. Если в процессе минимизации вычисление производных не производится, речь идет о поисковых методах.
Точка 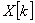 называется точкой k-го (очередного) приближения. Процесс отыскания точки
называется точкой k-го (очередного) приближения. Процесс отыскания точки 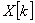 называется k-й итерацией.
называется k-й итерацией.
Большинство методов спуска определяется следующей итерационной формулой: 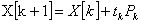 . Здесь: Pk – вектор, указывающий направление спуска на k-й итерации;
. Здесь: Pk – вектор, указывающий направление спуска на k-й итерации; 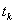 – скаляр, задающий величину шага вдоль выбранного направления.
– скаляр, задающий величину шага вдоль выбранного направления.