Пусть по-прежнему X = {0, 1}n для произвольного натурального n и r0 есть равномерное распределение вероятности на X, т.е. r0(x) = 2–n для всех x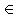 X. Функция f: {0, 1}*→{0, 1}* называется односторонней, если:
X. Функция f: {0, 1}*→{0, 1}* называется односторонней, если:
1) она полиномиально вычислима, т.е. существует такой вероятностный алгоритм α: {0, 1}*→{0, 1}*полиномиальной сложности (как функции от длины ее аргумента), что  x
x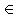 {0, 1}*(α(x) = f(x));
{0, 1}*(α(x) = f(x));
2) она полиномиально необратима, т.е. для любого вероятностного алгоритма A: {0, 1}*→{0, 1}* полиномиальной сложности (как функции от длины ее значения), для любого ε = 1/Q(n) и для всех достаточно больших n имеет место:
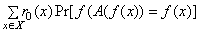 < ε.
< ε.Биективная односторонняя функция f, сохраняющая длину (т.е. обладающая свойством  x(|f(x)| = |x|)), называется односторонней подстановкой.
x(|f(x)| = |x|)), называется односторонней подстановкой.
Назовем h-c предикатом (от hard-core predicate) функции f: {0, 1}*→{0, 1}* полиномиально вычислимую функцию B: {0, 1}*→{0, 1}, полиномиально не вычислимую по f(x), т.е. такую, что для любого вероятностного алгоритма A: {0, 1}*→{0, 1} полиномиальной сложности (как функции от длины f(x)), для любого ε = 1/Q(n) и для всех достаточно больших n имеет место:
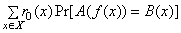 – 1/2 | < ε.
– 1/2 | < ε.Неформально, существование h-c предиката для f означает невозможность вычисления с полиномиальной сложностью одного бита аргумента функции по ее значению с вероятностью, непренебрежимо мало отличающейся от 1/2.