Цель работы: изучение явления интерференции света и определение длины световой волны.
Интерференцией волн называют явление, возникающее при наложении волновых процессов и проявляющееся в пространственном перераспределении энергии и образовании устойчивой картины колебаний с чередованием максимумов и минимумов интенсивности в различных точках пространства. Явление интерференции наблюдается только при сложении когерентных волн.
Пусть свет одинаковой частоты от двух источников до точки наблюдения проходит пути x
и x
в разных средах со скоростями v1 и v2 (показатели преломления сред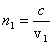 
и 
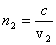, с – скорость света в вакууме). В точке наблюдения возникают колебания напряженности электрического поля (светового вектора) E1 и E2:
E1 = E10 sin [w(t - x1 /v1 )]= E10 sin [w(t - x1n1 /c )],
E2 = E20 sin [w(t - x2 /v2 )]= E20 sin [w(t - x2n2 /c )], (1)
где E
и E
– амплитуды складываемых колебаний, w – циклическая частота, xn и xn – оптические длины путей, с – скорость света в вакууме.
Если колебания векторов E1 и E2 имеют одинаковое направление, то амплитуда E0 суммарного колебания зависит от разности фаз складываемых колебаний.
, (2)
где λ – длина волны в вакууме, а 
– оптическая разность хода.
Если cos d = 0 всюду, то суммарная интенсивность света равна сумме интенсивностей, и интерференции не наблюдаются. Если cos d не изменяется со временем и принимает свое значение для каждой точки пространства, то будут наблюдаться интерференционные максимумы и минимумы света: максимумы в тех точках, в которых cos d = 1, и минимумы в тех, где cos d = -1.
Чтобы при наложении волн возникла интерференция, необходимы 2 условия:
1) колебания должны иметь постоянную разность фаз в течение всего времени наблюдения, при этом частоты интерферирующих волн должны быть одинаковы,
2) векторы E и E должны быть одинаково направлены, то есть волны должны иметь одинаковую поляризацию.
Волны, которые удовлетворяют этим условиям, называются когерентными (согласованными) волнами, а источники – когерентными источниками.
При сложении электромагнитных волн радиодиапазона, испущенных макроскопическими источниками – антеннами, проблемы когерентности не возникает: антенны просто должны удовлетворять этим двум условиям. Наложение волн светового диапазона от любых двух источников света (кроме лазеров) не дает интерференционной картины, так как эти источники всегда не когерентны. Если даже на два источника поставить одинаковые светофильтры и пропустить свет через поляризатор, чтобы сделать колебания E1 и E2 одинаково направленными, то интерференции света все равно не будет наблюдаться.
Это происходит потому, что источником света в действительном смысле этого слова является каждый отдельный атом. Любой технический источник света представляет собой на самом деле совокупность гигантского количества источников-атомов, которые постоянно «вспыхивают» и быстро «гаснут», причем случайным, не согласованным друг с другом образом. Время жизни такого источника-атома порядка 10-8 с. За это время свет проходит путь около 300 см, этот отрезок волны называют цугом волн.
Начальные фазы колебаний отдельных атомов независимы, поэтому разность фаз для разных цугов волн не постоянна, она быстро и беспорядочно меняется. Интерференционные приборы обладают инерционностью и, как правило, фиксируют среднюю амплитуду и интенсивность за время, гораздо большее 10-8 с, а для наблюдения интерференции необходимо, чтобы разность фаз исследуемых колебаний была постоянной в течение времени наблюдения.
Обеспечить постоянство во времени разности фаз можно двумя путями. Один заключается в том, чтобы согласовать акты излучения света атомами – это достигается в лазерах (вынужденное излучение). Второй путь – заставить интерферировать в точке наблюдения колебания от одного атома, приходящие в точку наблюдения по двум разным путям, посредством использования отражений и преломлений. На этом принципе основаны классические интерференционные схемы: зеркало Ллойда, бизеркала и бипризма Френеля. В этих схемах реализуется идея опыта Юнга: получить два когерентных источника для наблюдения интерференции путем деления пучка света, испускаемого одним источником, на два пучка.
Максимумы интерференции наблюдаются в тех точках, в которые интерферирующие волны приходят в одинаковой фазе, т.е. при d = 2pn, где n – целое число, положительное или отрицательное. Тогда разность хода равна:
D = nl. (3)
Минимумы наблюдаются в тех точках, в которые волны приходят в противофазе. Для этих точек разность фаз 
, что соответствует разности хода
. (4)
Для того чтобы максимумы и минимумы были более четкими, амплитуды складываемых колебаний должны быть равными. При наблюдении интерференции необходимо, чтобы разность хода волн была менее длины цуга. Иначе будут складываться колебания, создаваемые разными цугами, и условие когерентности выполняться не будет.
|
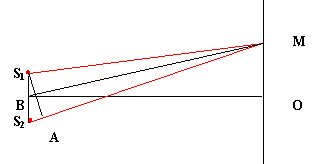
Рис. 1
|
Рассмотрим схему Юнга. Источниками света в оригинальном опыте Юнга являлись две узкие щели, интерференция наблюдалась на удаленном экране. На рис. 1 S1 и S2 – источники света, S1М и S2М – расстояния от источников до точки наблюдения М. Проведем S1А перпендикулярно S2М. Треугольники S1S2А и ВМО подобны. В практически применяемых интерференционных схемах угол между интерферирующими лучами S1МS2 мал (порядка долей градуса), т.е. расстояние от источников до экрана гораздо больше расстояния между самими источниками. Поэтому S2А приближенно равна разности хода D = S2М - S1М.
Из подобия треугольников имеем: D/d » x/L, откуда
x = LD/d, (5)
где х = ОМ – координата точки наблюдения на экране, d = S1S2 – расстояние между источниками, L = ВО – расстояние от источников до экрана.
Если в точке М наблюдается максимум, то разность хода лучей в этой точке равна целому числу длин волн. Тогда согласно (5) координаты точек максимумов равны 
(n – целое число: n = 0, ±1, ±2, ±3,…, называемое порядком интерференционного максимума). Между максимумами находятся минимумы. Расстояние между соседними максимумами и между соседними минимумами одинаково и равно
. (6)
Если на пути одного из лучей, например, верхнего, поставить тонкую прозрачную пластинку с показателем преломления n и толщиной h, то между лучами возникнет дополнительная оптическая разность хода 
, т.к. один из лучей проходит путь h в воздухе, а второй это расстояние проходит в веществе пластинки. Вследствие этого вся интерференционная картина сместится в ту сторону, где находится пластина, т.е. в нашем примере вверх. Если дополнительная разность хода равна длине волны, то произойдет смещение на ширину одной интерференционной полосы. Если произошло смещение картины на N полос (N может быть и дробным), то дополнительная оптическая разность хода:
. (7)
Эта формула позволяет, зная λ, определить как показатель преломления пластины (если известна толщина), так и ее толщину при известном показателе преломления.