Рассмотрим интерференцию в параллельных лучах. Экспериментальная установка изображена на рис.20.

Пучок параллельный лучей падает на николь-поляризатор Р и выходит с колебаниями, лежащими в плоскости его главного сечения. Пусть плоскость рисунка совпадает с плоскостью главного сечения николя-поляризатора Р. Между двумя николями помещена пластинка М из одноосного двупреломляющего кристалла, вырезанная параллельно оптической оси ОО'. Пусть свет падает на пластинку нормально. Только поляризованная волна, вышедшая из поляризатора Р , проходя через пластинку М, разделяется на две волны, поляризованные в двух взаимно перпендикулярных направлениях. Через пластинку эти волны проходят с разной скоростью, и, следовательно, приобретают на этом пути оптическую разность хода , где d – толщина пластинки, а n₀ и n_e – показатели преломления для обыкновенного и необыкновенного лучей. Анализатор А сведет колебания в этих лучах к одной плоскости и, таким образом, создаст условия для интерференции. Линза L₂ даст изображение на экране.

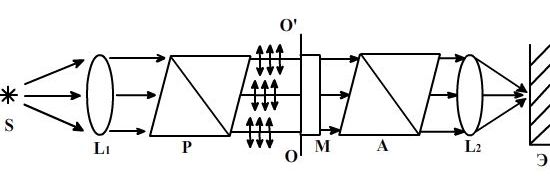
Рис.20

 

Рассмотрим интерференционную картину для различных случаев.

В двух случаях интерференции не будет: 1) когда плоскость главного сечения пластинки М совпадает с плоскостью главного сечения николя-поляризатора Р. В этом случае лучи пройдут как необыкновенные без деления на два;

2) когда плоскость главного сечения пластинки перпендикулярна плоскости главного сечения николя-поляризатора Р. В этом случае колебания в падающих лучах будут перпендикулярны плоскости главного сечения пластинки, и лучи пройдут как обыкновенные, без деления на два.

Если николи Р и А поставлены на свет, то поле зрения останется светлым, если на темноту, то будет темным.

Рис. 21

Теперь рассмотрим случай, когда главное сечение пластинки составляет угол α с главным сечением николя-поляризатора. На рис.21 Р, А и ОО' – плоскости главных сечений соответственно николя-поляризатора, николя-анализатора и пластинки М. Предположим, что николи скрещены(т.е. ) и через систему проходит параллельный пучок лучей. Тогда в луче, прошедшем через первый николь (Р), электрический вектор совершает колебания в направлении Р; амплитуда этих колебаний представляет модуль вектора Е. Попадая на пластинку М, световой луч разделяется на два – обыкновенный и необыкновенный, которые будут распространяться в пластинке в одном направлении, но с разными скоростями. Электрический вектор в необыкновенной волне совершает колебания в направлении ОО’, а обыкновенной волне – в направлении перпендикулярном к ОО'. Обозначим их Ее и Ео соответственно. Значения составляющих векторов Е получим, спроектировав его соответственно на направление ОО' и направление, к нему перпендикулярное. Так как плоскость главного сечения пластинки составляет угол α с главным сечением поляризатора, то

Е_е = Е cosα , Е_о = Е sinα.   (36)

Между колебаниями обоих лучей с амплитудами Е_е, Е_о возникает разность фаз

(37)

Николь-анализатор пропустит лишь колебания, представляющие собой проекцию колебаний Е_е и Е_о на направления А. Амплитуды этих колебаний изобразятся на рис.21 – Е_е1, Е_о1. Из рис. 21 и равенства 36 имеем

Е_е1=Е_е sinα=Е sinα cosα         (38)

Е_о1=Е_о cosα=Е sinα cosα        (39)

Таким образом, амплитуды Е_е1, Е_о1 равны друг другу, но направлены в противоположные стороны, следовательно, между соответствующими им колебаниями кроме разности фаз Δφ, определяемой формулой (37), имеется еще дополнительная разность фаз π. Значит, суммарная разность фаз Δφ₁ равна

(40)

Если Δφ₁=2кπ, где к - целое число, то оба колебания усиливают друг друга, и поле при рассмотрении сквозь скрещенные николи окажется просветленным.

При Δφ₁=(2к+1)π колебания полностью погасают друг друга и поле становиться темным. При освещении системы белым светом условие максимального усиления или ослабления колебаний осуществляется не одновременно для лучей разных длин волн λ, и поэтому при заданной толщине плоскопараллельной пластинки, расположенной между скрещенными николями, поле представляется равномерно окрашенным. Тон окраски зависит от толщины пластинки d и значения коэффициентов преломления (n_o-n_e).

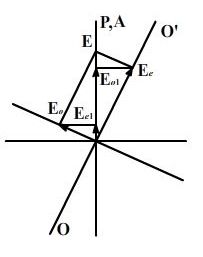
Рис 22.

Рассмотрим теперь случай, изображенный на рис. 22, когда главные сечения николей расположены параллельно друг другу (Р||А).

Из рис. 22 видно, что

Е_е1 = Е_е cosα = Е cos²α,         (41)

Е_о1 = Е_о sinα = Е sin²α.         (42)

Оба вектора Е_е1, Е_о1 направлены в одну сторону, и разность фаз между соответствующими им колебаниями равна

(43)

т.е., отличается на π от разности фаз Δφ₁. При любом значении угла α, кроме α=±π/4, амплитуды Е_е1, Е_о1 теперь не равны и , следовательно, ни при какой толщине пластинки колебания не могут полностью погасить друг друга. При любой толщине пластинки, расположенной между параллельными николями (и любом значении (n_o-n_e)) поле окажется более или менее просветленным и окрашенным. Только при α=±π/4 при параллельных николях, амплитуды Е_е1, Е_о1 равны друг другу. В этом случае пластинка, введенная между николями, может погасить свет.

Благодаря тому, что разность фаз Δφ₂ отличается на π от разности фаз Δφ₁, при параллельных николях ослабляются те лучи, которые при той же пластинке усилились при скрещенных николях, и наоборот. При наблюдении в белом свете будут теперь гасится те волны, которые давали наибольший вклад в окраску пластины в случае скрещенных николей и окраска пластины будет дополнительной до белой по отношению к той окраске, которую пластинка имела при наблюдении при скрещенных николях. Окраска непрерывно меняется, если поворачивать один из николей или пластинку (николи остаются неподвижными). Описанное явление носит название хроматической поляризации. Интерференция поляризованных лучей используется в поляризационном микроскопе и других поляризационных приборах.