Теория вращения плоскости поляризации веществом была предложена Френелем в 1817 г.Френель считал, что в оптически активных веществах наблюдается особый вид двойного лучепреломления, который состоит в том, что падающая плоско поляризованная световая волна в этих веществах разделяется на две кругополяризованных волны, которые распространяются в одном направлении, но с разными фазовыми скоростями. Это означает, что плоско поляризованная световая волна, падающая на оптически активное вещество, распадается в нем на две волны, поляризованные по кругу с противоположным направлением вращения с одинаковыми амплитудами и с разными скоростями распространения: V_d для волны с правым вращением (d от слова droit - правый), V_g - с левым вращением (g от слова gauche - левый). Соответственно и показатели преломления вещества n_d и n_g для этих волн будут различны.

Рассмотрим слой оптически активного вещества толщиной l. На входе в это вещество линейно поляризованный луч разлагается на две волны той же частоты, но поляризованные по кругу с левым и правым вращением. Электрические векторы этих волн E_d и E_g численно равны половине амплитуды вектора Е и вращаются с угловой скоростью ω (ω - циклическая частота колебаний в падающей волне) соответственно против и по часовой стрелке (если смотреть навстречу лучу). Это означает, что в любой момент времени в данной точке они симметричны относительно плоскости ОО' падающей световой волны (рис. 18).

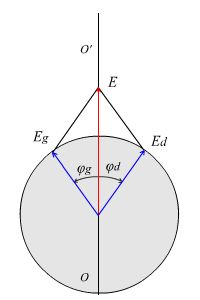
Рис. 18

Какова будет взаимная ориентация этих векторов в произвольной точке среды относительно направления вектора Е в падающей волне? В каждой точке среды, до которой доходят колебания, вектора Е_d и Е_g вращаются с угловой скоростью ω, равной циклической частоте колебаний. В оптически активном веществе скорости V_d и V_g циркулярно поляризованных волн Е_d и Е_g различны. Предположим, что V_d > V_g. Тогда, так как левая волна распространяется с меньшей скоростью, то до любой точки внутри вещества она дойдет с некоторым отставанием по фазе по отношению к правой. Если за время t=nT (cчитая, что за Т совершается один полный оборот) колебание вектора E_d дошло до точки А и имеет направление, совпадающее с вектором Е входящей волны, то вектор Е_g левой волны еще не дошел до заданной точки. Так как вектор Е_d в точке вращается, то пока левая волна дойдет до этой точки, имея направление вектора Е входящей волны, вектор E_d повернется на угол φ_d. При сложении векторов E_d и Е_g в этой токе плоскость колебаний Е повернется вправо на угол ψ относительно ОО'. Так как оба вектора Е_d и Е_g в произвольной точке внутри вещества вращаются с одинаковыми угловыми скоростями, то результирующий вектор Е будет совершать линейное колебание в плоскости, повернутой на угол ψ относительно первоначальной.

Таким образом, плоскость колебаний вектора Е линейно поляризованного луча по мере прохождения через оптически активное вещество со значением n_d = n_g будет непрерывно поворачиваться в пространстве.

Для аналитического решения этой задачи запишем уравнение для волн с левым и правым вращением:

,  (32)

(33)

Поскольку вектора Е вращаются с угловой скоростью, равной частоте колебаний ω, и распространяются с разными фазовыми скоростями, то время вращения векторов в точке на расстоянии l от точки О(на входе волны в вещество) меньше на l /V_d или на l/V_g,чем время вращения векторов в точке О. Поэтому угол поворота вектора Е в точке на расстоянии от входа l равен фазе волны в данной точке, то есть

.  (34)

Если V_d > V_g,то на выходе из вещества вектор V_d обгоняет по фазе вектор V_g, то есть электрический вектор правой волны будет повернут вправо на большой угол, чем вектор левой волны. Следовательно, плоскостью, относительно которой симметрично расположены оба вектора, будет плоскость ВВ', повернутая по отношению к ОО' на угол ψ.

 

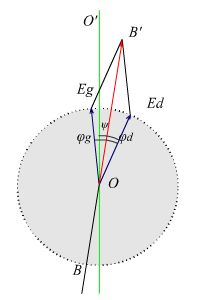
Рис. 19

Как видно из рис. 18, φ_d-ψ=φ_g+ ψ, то есть . Используя выражение (34), угол поворота плоскости поляризации получаем
,   (35)

где λ - длина волны в вакууме.

Как видно из формулы (35), для веществ, у которых n_g >n_d, плоскость поляризации поворачивается вправо (φ_d>φ_g) - правовращающие вещества, а для веществ, у которых n_g<n_d, - влево (φ_d <φ_g) - левовращающие вещества.

Итак в рамках теории Френеля вращение плоскости поляризации получило объяснение. Однако эта теория не вскрыла причины разбиения линейно поляризованного луча на два циркулярно поляризованных и причины различия фазовых скоростей волн с левым и правым вращением в оптически активном веществе.

С молекулярной точки зрения это объясняется асимметрией молекул либо асимметричным размещением атомов в кристалле. Оказывается, что все оптически активные вещества существуют в двух разновидностях – левовращающей и правовращающей. Молекулы и кристаллы одной разновидности являются зеркальным отражением молекулы и кристалла другой. Обе эти разновидности отличаются только направлением вращения плоскости поляризации. В 1915 году Борн показал, что, исходя из общей модели молекулы (отрезок спирали), пригодной для истолкования молекулярной анизотропии вообще, можно объяснить и вращение плоскости поляризации асимметричными молекулами, то есть молекулами, не имеющими ни центра симметрии, ни плоскости симметрии.

Физики В.Р. Бурман и А.В. Тиморева дополнили теорию, показав, что в явлении вращения плоскости поляризации существенную роль играет также магнитный момент, индуцируемый в асимметричной молекуле магнитным полем световой волны.