Пусть на пластинку из одноосного кристалла, вырезанную параллельно его оптической оси, падает нормально плоскополяризованный свет. На рис.15 плоскость пластинки совпадает с плоскостью рисунка. Свет падает перпендикулярно плоскости рисунка в точку О. Направление колебаний электрического вектора в падающем поляризованном луче составляет угол α с направлением оптической оси пластинки ОХ.
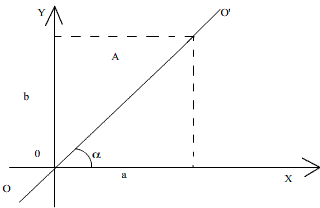 Рис.15
Рис.15
Если обозначим через А амплитуду падающей волны, то амплитуды колебаний в необыкновенной и в обыкновенной волнах будут соответственно равны
![]()
Сложение двух взаимно перпендикулярных колебаний с разными амплитудами и разностью фаз приведет к возникновению эллиптического колебания, то есть колебания, при котором конец результирующего вектора описывает эллипс в плоскости волнового фронта с той же угловой частотой ω, с которой совершаются исходные колебания.
Действительно, колебания в волнах, прошедших пластинку, описываются соотношениями
![]()
Чтобы получить траекторию результирующего колебания, надо из этих уравнений исключить время t. Это можно сделать, например, таким образом. Из (21), (22) имеем
![]()
или
![]()
Возводя правую и левую части в квадрат и складывая с
![]()
Получим
![]() (23)
(23)
Это уравнение эллипса (кривая 1 на рисунке 16).
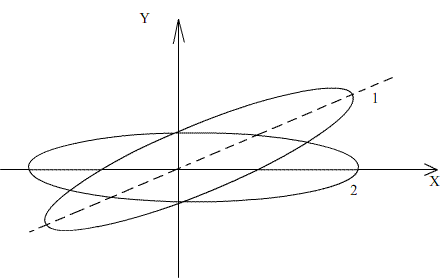
Рис.16
Таким образом, после прохождения линейно поляризованного света через кристаллическую пластинку получаем, вообще говоря, световую волну, конец вектора Е которой описывает эллипс. То есть получаем эллиптически поляризованный свет. Форма эллипса и ориентация его относительно осей х и у зависят от значений амплитуд необыкновенной и обыкновенной волн а, b(которые определяются углом α) и разностью фаз φ. А разность фаз φ, в свою очередь, для данной величины лучепреломления |nе-n0| пропорциональна толщине кристаллической пластинки d (см.(20)).
Рассмотрим два частных случая.
1. Толщина пластинки такова, что разность хода двух волн составляет четверть длины световой волны (пластинка в 1/4 волны):
![]()
или, в общем случае,
![]() (24)
(24)
Тогда, согласно (20), φ = π /2 или φ =(2m+1) π/2 и уравнение эллипса примет вид
![]() (25)
(25)![]()
Т.е. мы получили эллипс, ориентированный относительно оптической оси (полуось а расположена вдоль оптической оси, кривая 2 на рис.16). Соотношение длин полуосей а и b зависит от угла α. В частности, при α = 45° находим a = b, так что эллипс обращается в окружность, описываемую уравнением
![]() (26)
(26)
В данном случае свет поляризован по кругу.
2. Пластинка такова, что разность хода двух лучей составляет половину длины световой волны (пластинка в 1/2 волны):
![]() (27)
(27)
или, в общем случае,
![]() (28)
(28)
Тогда или . В этом случае эллипс вырождается в прямую
![]() (29)
(29)
Прошедший свет остается линейно поляризованным, как и падающий луч, но, согласно уравнению прямой направление колебания переходит, например, из 1-го и 2-го квадранта во 2-й и 4-й квадранты. В частности, если 45°, то а = b, и уравнение прямой (29) будет x = – y (30) т.е. результирующее направление колебаний также составляет угол 45° с осями X и Y, но во втором квадранте направление колебаний по сравнению с падающим лучом повернулось на 90°. Таким образом, пластинка в 1/2 волны поворачивает плоскость поляризации света на некоторый угол, а в случае α = 45° поворот будет равным 90°.
На основании изложенного можно проследить следующую общую картину изменения поляризации света в результате прохождения пластины.
Пусть а≠0 и b≠0, т.е. угол α≠0 и π/2. Тогда с увеличением толщины, пластины d поляризация вышедшего луча проходит следующие стадии (рис.17).
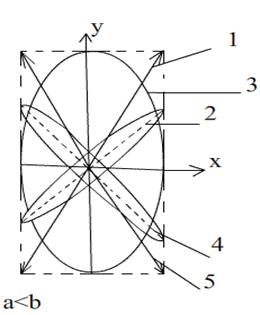
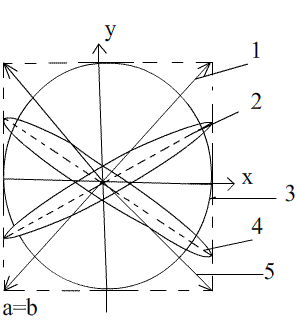
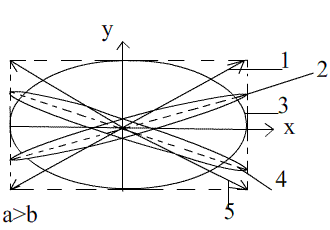
Рис.17
Падающий луч плоскополяризован (на рис.17 это прямая 1). С увеличением d поляризация становится эллиптической (кривая 2), причем наклон оси эллипса по отношению к оптической оси х по мере роста d уменьшается, и сам эллипс становится шире (растет малая полуось). При достижении пластинкой толщины, при которой (nе - n0 ) d = (1/4) λ, эллипс (кривая 3) оказывается ориентированном по отношению к осям х и у (то есть а и b располагаются вдоль осей х и у). При этом, если а = b, то эллипс переходит в окружность. При дальнейшем увеличении d эллипс сужается и занимает положение 4 и, наконец, вырождается в прямую 5. Угол наклона прямой 5 по отношению к оптической оси х оказывается равным , то есть таким же, как и для прямой 1, только сама прямая теперь проходит через 2-ой и 4-ый квадранты. Если α = 45° и , следовательно, a = b, то прямые 1 и 5, соответствующие начальной и конечной линейной поляризации, будут взаимно перпендикулярны.