Алгоритм  для построения таблицы анализа М может применен к любой грамматике. Однако для некоторых грамматик может иметь неоднозначно определенные входы. Например, если грамматика леворекурсивна или неоднозначна, М будет иметь крайней мере один неоднозначно определенный вход.

Грамматики, для которых таблицы анализа не имеют неоднозначно определенных входов, называются LL(1). Первое L означает сканирование входа слева- направо, второе L означает, что строится левый вывод, 1 — что на каждом шаге для принятия  решения используется один символ непросмотренной цепочки. Можно показать, что алгоритм  для  каждой  LL(1) -грамматики строит таблицы, по которым распознаются все цепочки из  L(G) и только они.

LL(1) -грамматики имеют несколько отличительных свойств.

Неоднозначная или леворекурсивная грамматика не может быть LL(1). Можно также показать, что грамматика G является LL(1) тогда и только тогда, когда для двух правил вида А->u|v

выполняется следующее:

1) ни для какого терминала а одновременно из u и v не выводятся строки, начинающиеся с а;

2) только из одной из строк u или v может выводиться пустая строка;

3) если v=>*e, то из u не выводится никакая строка, начинающаяся с терминала из FOLLOW(A).

Эквивалентным является следующее определение:

КС грамматика называется LL(1)-грамматикой, если из существования двух левых выводов

(1) S=>*w Au=>w v w u=>* wx,

(2) S=>* w A u =>w z u =>* wy,

для которых FIRST(x)=FIRST(y), вытекает, что v=z. Это означает, что для данной цепочки wAu и первого символа, выводящегося из Аu (или $), существует не более одного правила, которое может быть применено к А, чтобы получить вывод какой-нибудь терминальной цепочки, начинающейся с w и продолжающейся этим первым символом. Язык, для которого можно построить LL(1) -грамматику, называют LL(1) -языком. Если таблица анализа имеет неоднозначно определенные входы, грамматика не является LL(1). Примером может служить следующая грамматика:

St -> if Ex then St

if Ex then St else St

Cont

Ex->...

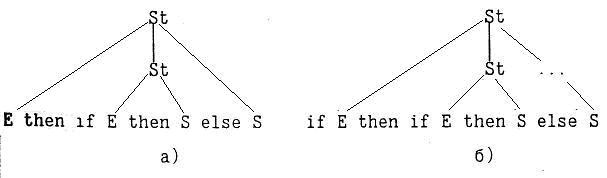
Эта грамматика неоднозначна, что иллюстрируется рисунком 66.

Рисунок 66

 

Поскольку грамматика неоднозначна, она не является LL(1) . Проблема, порождает ли грамматика LL-язык, алгоритмически неразрешима.