Приведем теперь алгоритм построения детерминированного конечного автомата по регулярному выражению. К регулярному выражению (сокращенно PB) r добавим маркер конца: (r)#. После построения ДКА для расширенного РВ легко построить ДКА для исходного РВ: все состояния ДКА, из которых есть переход в конечное с чтением символа "#", можно считать конечными, а символ "#" и соответствующие переходы удалить.

Представим РВ в виде дерева, листья которого — терминальные символы, а внутренние вершины- операции "." (конкатенации), "U" (объединение), "*" (итерация).

Каждому листу дерева (кроме е-листьев) припишем уникальный номер и ссылаться на него будем, с одной стороны, как на позицию в дереве и, с другой стороны, как на позицию символа,. соответствующего листу.

Теперь, обходя дерево Т сверху-вниз слева-направо, вычислим четыре функции: nullable, firstpos, lastpos, followpos. Функции nullable, firstpos и lastpos определены на узлах дерева, а followpos - на множестве позиций. Значением всех функций, кроме nullable, является множество позиций. Функция followpos вычисляется через три остальные функции.

Функция firstpos(n) для каждого узла n синтаксического дерева регулярного выражения дает множество позиций, которые соответствуют первым символам в подцепочках, генерируемых подвыражением с вершиной в n. Аналогично, lastlog(n) дает множество позиций, которым соответствуют последние символы в  подцепочках, генерируемых подвыражениями с вершиной п. Для узлов n, поддеревья которых ( т.е. дерево, у которого узел n является корнем) могут породить пустое слово, определим nullable(n)=true, а для остальных узлов false.

Таблица для вычисления функций nullable и firstpos приведена на рисунке 54. Вычисление функции lastpos строится аналогично.

 

Рисунок 54

Пример. Функции firstpos  и lastpos для выражения (a+b)abb# приведены на рисунке 55. Слева от каждой вершины значение firstpos, справа- lastpos. Заметим, что эти функции могут быть вычислены за один проход дерева.

Если i- позиция, то followpos(i) есть множество позиций j таких, что существует некоторая строка ...cd..., входящих в язык, описываемый PB, такая, что i соответствует этому вхождению c, а j- вхождению d.

Функция followpos может быть вычислена также за один обход дерева по следующим двум правилам.

1. Пусть n - внутренний узел с операцией "." (конкатенация), a, b - его потомки. Тогда для каждой позиции i, входящей в lastpos(a), добавляем к множеству значений  followpos(i) множество  firstpos (b).

2. Пусть n — внутренний узел с операцией "*" (итерация), а – его потомок. Тогда для каждой позиции i, входящей в lastpos (а),  добавляем к множеству значений followpos(i) множество  firstpos(a).

Для примера  значения функции followpos приведены на рисунке 55.

 

Рисунок 55

Функция followpos позволит теперь сразу построить детерминированный конечный автомат с помощью следующего алгоритма.

Алгоритм. Прямое построение  ДКА по регулярному выражению.
Будем строить множество состояний автомата  Dstates и помечать их. Состояния ДКА соответствуют множествам позиций. Начальным состоянием будет состояние  firstpos(root), где root - вершина синтаксического дерева регулярного выражения, конечными — все  состояния, содержащие позиции, связанные с символом "#".

Сначала в Dstates имеется только одно непомеченное состояние firstpos(root).

while есть непомеченное состояние Т в  Dstates do

пометить Т;

for каждого входного символа а<-Т do

пусть символу а в Т соответствуют позиции

р₁ ,...,р_i, и пусть  S=U_i followpos(p_i)

Если S не пусто и S не принадлежит  Dstates, то

добавить непомеченное состояние S в  Dstates (рисунок 56)

Функцию перехода  Dtran для Т и а определить как Dtran(T,a)=S.

end;

end;

 

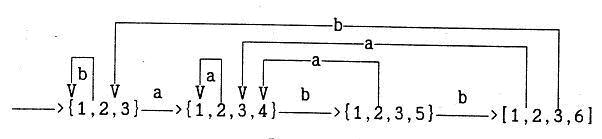
Для нашего примера вначале Т={1(f),2(b),3(a)}. Последовательность шагов алгоритма приведена на рисунке 56. В результате будет построен детерминированный конечный автомат, изображенный на рисунке 57. Состояния автомата обозначаются как множества позиций, например {1,2,3}, конечное состояние заключено в квадратные скобки [1,2,3,6].

 

Рисунок 56

 

Рисунок 57