В некоторых языках за основу записи арифметических выражений взята польская запись; она имеет преимущества при переводе в машинные команды, но несколько необычна для понимания ее человеком. Польской она называется потому, что впервые была введена польским философом Лукашевичем- в связи с формулами символической логики. В настоящее время среди занимающихся машинной математикой более распространена- разновидность польской записи, называемая «обратной польской записью».
Когда операция появляется между своими операндами, как в выражении a+b, про нее говорят, что это двусторонняя операция. -При вычислении выражения
З*5+7*11 (12)
необходимо учитывать, что операция умножения «связывает» опе-ранды сильнее, чем операция сложения; вычисление может быть выполнено с помощью «стека» и команд, использующих только один или два верхних элемента стека.
Команды Стек («вершина» справа)
Взять 3 3
Взять 5 3 5
Умножить 15
Взять 7 15 7
Взять 11 15 7 11
Умножить 15 77
Сложить 92
Сокращенно процесс вычисления можно записать следующим образом-:
3 5 * 7 11 * + (13)
что является преобразованием выражения (12). Соответствующее преобразование выражения
(З * 5+7)*11 (14)
будет иметь вид
3 5*7 +11*х (15)
Видно из этих примеров и можно доказать в общем случае, что запись в форме (13) определяет процесс вычисления однозначно, несмотря на отсутствие в ней каких-либо скобок. Выражения (13) и (15) приведены в форме обратной польской записи и они эквивалентны стандартной записи в форме (12).
Обратная польская запись базируется на структуре <операнд ><операнд> <операция>, или на структуре с правосторонней операцией; прямая польская запись аналогично этому базируется на структуре с левосторонней операцией- <операция> <операнд><операнд>,— и наши примеры в форме прямой польской записи имеют вид
+*3 5*7 11 (16)
*+*3 5 7 11 (17)
Первый из них можно интерпретировать таким образом: сложить (умножить (3, 5), умножить (7, 11)). Так же как и для случая обратной польской записи, эти примеры свободны от неоднозначности при вычислении и не содержат скобок.
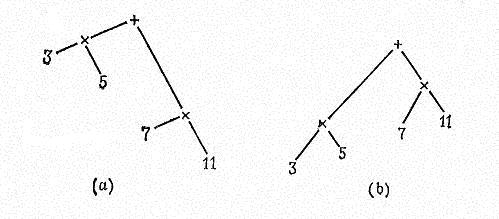
Рисунок 19. Представление польской записи в виде графа
Показательна диаграмма на рисунке 19а; если символьные элементы диаграммы спроектировать влево и затем прочитать сверху вниз, то мы получим прямую польскую запись; проекция на горизонтальную линию вниз дает запись в обычной алгебраической форме. Диаграмма на рисунке 19b, топологически эквивалентная предыдущей, при проектировании влево и чтении снизу вверх дает обратно польскую запись.
Так как порядок элементов в обратной польской записи - это тот самый порядок, в котором элементы должны выбираться при обработке, то очевидно, что преобразование в обратную польскую запись (подходящим образом обобщенную) неявно присутствует любой компиляции. Поскольку речь идет об алгебраических выражениях, такое преобразование может быть выполнено следующим алгоритмом:
Z: Занести очередной элемент в А
If в А объект, выдать его и goto Z else
If в А закрывающая скобка then разгрузить стек до открывающей скобки, убрать обе скобки и go to Z else
Y: if элемент связывает сильнее, чем верхний элемент стека, или является открывающей скобкой then занести его в стек и goto Z else выдать операцию из вершины стека и goto Y
При соответствующих усовершенствованиях этого алгоритма он может быть использован для компиляции самых различных синтаксических структур.
Простое арифметическое выражение с вещественными перемен-ными
A+b*c-d/(a+b)
можно графически представить в виде дерева (рисунок 20).
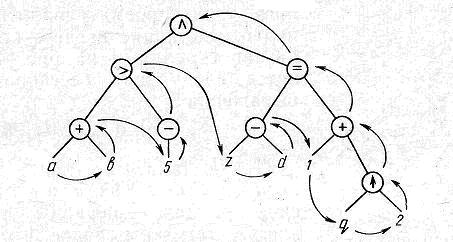
Рисунок 20. Порядок обхода дерева арифметического выражения для получения обратной польской записи
Узлы дерева соответствуют операциям, а ветви- операндам. Левая ветвь, исходящая из узла, отвечает левому операнду, а правая- правому. В каждой ветви операциям, которые выполняется рань-ше, соответствуют нижележащие узлы. Верхний узел (корень де-рева) отвечает операции, которая выполняется последней. С него начинается построение дерева.
Если, начав с нижнего листа самой левой ветви дерева, обойти все листья и узлы дерева так, чтобы ветви рассматривались слева направо, а узел рассматривался только после обхода всех исходящих из него вет-вей, как показано стрелками на рисунке 20, то последовательность просмотра листьев и узлов даст обратную польскую запись исходного выражения:
Abc*+dab+/-.
Такую бесскобочную запись, как мы уже знаем, называют также постфиксной записью, потому что знак каждой операции записан после соответствующих операндов.
Заметим, что в обратной польской записи операнды располагаются в том же порядке, что в исходном выражении, а знаки операций при просмотре записи слева направо встречаются в том порядке, в котором нужно выполнять соответствующие действия. Отсюда вытекает основное преимущество обратной польской записи перед обычной записью выражений со скобками: выра-жение можно вычислить в процессе однократного просмотра слева направо. Правило вычисления выражении в обратной польской записи состоит в следующем. Обратная польская запись просматривается слева направо. Если рассматриваемый элемент - операнд, то рас-сматривается следующий элемент. Если рассматриваемый эле-мент — знак операции, то выполняется эта операция над операн-дами, записанными левее знака операции. Результат операции записывается вместо первого (самого левого) операнда, участво-вавшего в операции. Остальные элементы (операнды и знак опера-ции), участвовавшие в операции, вычеркиваются из записи. Про-смотр продолжается.
В результате последовательного выполнения этого правила бу-дут выполнены все операции, имеющиеся в выражение, и запись сократится до одного элемента — результата вычисления выражения.
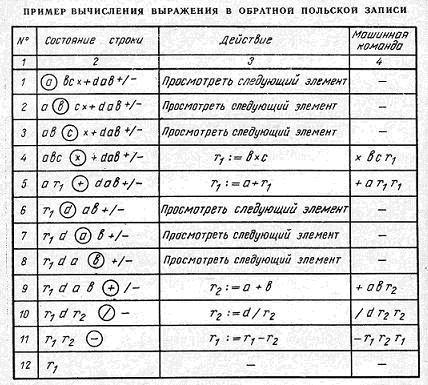
Выполнение правила для нашего примера приводит к последо-вательности строк, записанных во второй графе таблицы 7.
Таблица 7.
Рассмат-риваемый на каждом шаге процесса элемент строки отмечен круж-ком. В третьей графе таблицы записаны соответствующие действия, а в четвертой графе — эквивалентные команды трехадресной –машины.
Результат выполнения операции фиксируется в виде рабочей переменной вида rj. После очередной операции рабочая переменная r1 или r2 вычеркивается, освободившуюся рабочую переменную можно использовать вновь для записи результата операции. Использование каждый раз свободной рабочей переменной с минимальным номером экономит количество занятых рабочих переменных. Такой пример экономии рабочих ячеек приведен в таблице 7. Это же правило используют в трансляторах.
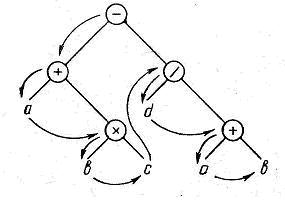
Существует еще одна форма бесскобочной записи выражений, которая также иногда применяется в трансляторах. На рисунке 21 изображено то же дерево, что и на рисунке 20. Если, начав с верхнего узла, обойти все узлы и листья дерева так, чтобы верхний узел рас-. сматривался раньше нижнего и сразу после рассмотрения очередного узла просматривались слева на-
право исходящие из него ветви, как показано стрелками на рисунке 21, то полу-чится следующая бесскобочная запись выражения - + а* bc/d + ab, т.е. прямая польская запись. Как и в обратной польской записи, операнды расположены здесь в том же порядке, что в исходном
Рисунок 21. Порядок обхода дерева арифметического выражения для получения прямой польской записи выражении.
Однако знаки операций теперь записаны перед операндами, поэтому такую запись называют также префиксной. - Выражение, записанное в прямой польской записи, вычисляется справа налево. Поскольку общий порядок работы компилятора обычно слева направо, прямую польскую запись применяют относительно редко.