Совокупность всех сил, действующих на точки материальной системы, можно разделить на внутренние и внешние силы.

Внутренние силы –  это силы взаимодействия между точками системы.

Внешние силы – это силы, действующие на точки системы со стороны других точек, не входящих в систему.

Пусть – равнодействующая всех сил, приложенных к точке .

.

Сумма называется главным вектором системы сил.

– главный вектор внутренних сил,

где 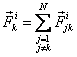– сумма внутренних сил, действующих на k-ю точку системы,

где, в свою очередь, – сила, действующая на k–ю точку со стороны j-й точки системы.

Свойство главного вектора внутренних сил:

,

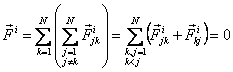т.к. в силу третьего закона Ньютона .

– главный вектор внешних сил,

где – сумма внешних сил, действующих на k-ю точку системы со стороны других тел, не входящих в систему. Если , то система называется замкнутой или изолированной.

Таким образом, главный вектор системы сил, действующих на СМТ, равен главному вектору внешних сил:

.

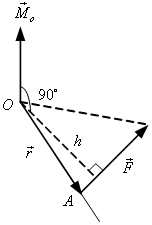Рис. 1.5. Момент силы

Отсюда не следует, однако, что все внутренние силы взаимно уравновешиваются и не влияют на движение системы. Они приложены к разным материальным точкам и могут вызывать взаимное перемещение этих точек. Это утверждение справедливо лишь для абсолютно твердого тела.

Моментом силы относительно точки О называется вектор , равный вектору произведения радиуса-вектора точки A приложения силы относительно точки О на вектор силы (рис. 1.5). Из свойств векторного произведения следует , где – плечо силы.

Используется также символическая запись векторного произведения

,

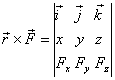позволяющая быстро получить проекции на координатные оси:

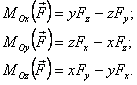
Моментом силы относительно оси z называется проекция на эту ось момента силы относительно любой точки, взятой на этой оси.

Введем понятие главного момента системы сил.

Пусть – равнодействующая всех сил, приложенных к точке механической системы, а – радиусы-векторы точек относительно точки О. Тогда главным моментом системы сил относительно точки О называется сумма

Легко показать, что главный момент внутренних сил равен нулю (также из третьего закона Ньютона)

,

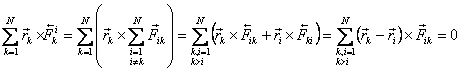т.к. .

Таким образом,   главный момент системы сил, действующих на СМТ, равен главному моменту внешних сил:

.

Примечание.

В частном случае, если рассматривается твердое тело, то с помощью введенных понятий главного вектора и главного момента можно сформулировать условия равновесия произвольной системы сил, приложенных к твердому телу, позволяющие решать многие задачи статики: для равновесия твердого тела, находящегося под действием произвольной пространственной системы сил, необходимо и достаточно, чтобы главный вектор и главный момент этой системы, относительно произвольного центра приведения, были равны нулю, т.е.

;  .

Эти же равенства дают необходимые, но недостаточные условия равновесия любой изменяемой механической системы (например, СМТ). При этом используется принцип отвердевания: если изменяемая система тел находится в равновесии, то это состояние не может быть нарушено присоединением дополнительных связей между точками и телами системы. Следуя этому принципу при составлении необходимых условий равновесия, любую изменяемую систему можно рассмотреть как абсолютно твердое тело.

Конец примечания.