В зависимости от значения числа Рейнольдса течение вязкой жидкости может иметь различный характер.

1. Пусть Re<<1, т.е. инерционные силы малы по сравнению с силами вязкости, и ими можно пренебречь.

Тогда уравнение Навье–Стокса для стационарного движения несжимаемой жидкости (2.42) приобретает вид

.

(2.49)

Это уравнение называется уравнением Стокса для «ползущих» течений. К этому классу относятся медленное течение вязкой жидкости, движение жидкости с большой вязкостью, движение малых тел в вязких жидкостях. Это уравнение линейно, поэтому строить его решение проще.

Пример.

Рассмотрим обтекание сферы при малых числах Рейнольдса установившимся потоком, скорость которого на бесконечности направлена параллельно оси x (рис. 2.7).

Рис. 2.7. Обтекание сферы при малых Re [11]

Тогда замкнутая система уравнений:

;

.

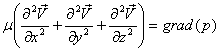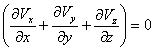Граничные условия на сфере :  или

; ; ;

на бесконечности

; ; ; .

Решение этой системы имеет вид

;

;

; ,

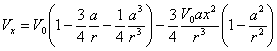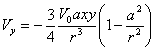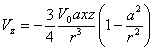где .

По этому решению можно вычислить силу сопротивления сферы в потоке:

,

где – компоненты первой строки тензора напряжений.

После интегрирования получается известная формула Стокса для сопротивления сферы при малых Re:

.

Коэффициент сопротивления сферы тогда

.

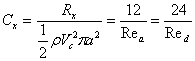Но полученное решение оказывается неприемлемым на достаточно больших расстояниях от шара, несмотря на малость числа Рейнольдса, т.к. там сказываются погрешности из-за отбрасывания члена