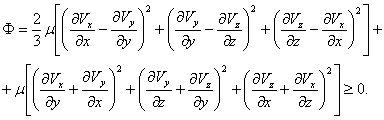Рассмотрим уравнение энергии вязкой жидкости в форме (2.40)

.

Отличие от аналогичного уравнения для идеальной жидкости (2.24) – в скалярном слагаемом и слагаемом, связанном с вектором теплового потока .

Распишем первое из указанных слагаемых покоординатно:

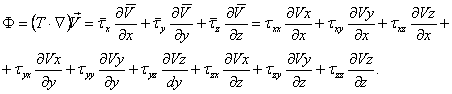
Подставив в него компоненты тензора вязких напряжений

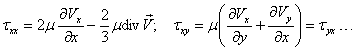и т.д., после преобразования получаем

(2.43)

Физический смысл этой величины – удельная мощность деформации, т.е. отнесенная к единице времени и единице объема та часть работы сил вязкости, которая расходуется на деформацию жидкого объема. Ее также называют диссипативной функцией.

В частном случае для несжимаемой жидкости ) диссипативная функция имеет вид

,

(2.44)

где .

Внутренняя энергия несжимаемой жидкости где С – массовая теплоемкость.

Тогда уравнение энергии

.

Если предположить, что теплообмен с окружающей средой  происходит по закону Фурье и то уравнение энергии несжимаемой вязкой ньютоновской жидкости примет вид

или  ,

(2.45)

где – коэффициент температуропроводности . Он характеризует скорость изменения (выравнивания) температуры вещества в неравновесных тепловых процессах.

Если рассматривать еще более частный случай – среда неподвижна (), то получаем известное уравнение теплопроводности в неподвижной среде (например, в твердом теле)

.

Судя по выражению (2.43) диссипативная функция является неотрицательной величиной: , причем нулевое значение реализуется при условии покоя.

Это говорит о том, что при отсутствии теплообмена с внешней средой () прирост энтропии, выражающей необратимость перехода механической энергии потока несжимаемой вязкой жидкости в тепло, всегда больше нуля, т.к. в этом случае, исходя из первого и второго начал термодинамики, имеем , и уравнение энергии запишется в виде

.

Следовательно, движение вязкой теплоизолированной несжимаемой жидкости всегда сопровождается потерей механической энергии. Поэтому приведенная в движение и предоставленная сама себе вязкая жидкость рассеивает сообщенную ей механическую энергию по всей жидкости до тех пор, пока не остановится.

Переход части энергии упорядоченных процессов (например, кинетической энергии движущегося тела) в энергию неупорядоченных процессов (в конечном счёте в теплоту) называется диссипацией энергии. Системы, в которых происходят такие процессы, называются диссипативными. Если диссипация энергии происходит в замкнутой системе, то (как это было показано), энтропия системы возрастает.

Диссипация осуществляется двумя отличными друг от друга процессами:

– конвекцией – это макроперенос: перенос энергии потоком жидкости (различают естественную конвекцию (при перепаде температур) и вынужденную конвекцию (под действием каких-то внешних сил);

– диффузией (теплопроводностью) – это микроперенос: перенос энергии молекулами и атомами в процессе их теплового движения.

Соотношение между интенсивностью теплообмена за счёт конвекции и интенсивностью теплообмена за счёт теплопроводности показывает число Нуссельта . Это число – один из основных критериев подобия тепловых процессов (см. п. 2.4.7).

Диссипация энергии в открытых системах, обусловленная процессами уноса энергии, например в виде излучения (), может приводить к уменьшению энтропии рассматриваемой системы при увеличении полной энергии системы и окружающей среды.