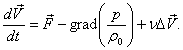Уравнения движения вязкой ньютоновской жидкости несколько упрощаются, если считать коэффициент вязкости величиной постоянной =const.

Подставим в уравнение движения выражение для тензора вязких напряжений

.

Если взять соответствующие производные от компонент тензора скоростей деформации, то после несложных преобразований выражение для запишется в виде

,

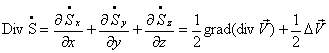где .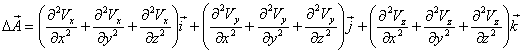

Подставляя его в уравнение, получим

.

(2.41)

Это уравнение носит название уравнения Навье–Стокса по имени французского физика Анри Навье и британского математика Джорджа Стокса, получивших и исследовавших его.

Проецируя на оси декартовой системы координат, получаем уравнения Навье–Стокса в проекциях:

.

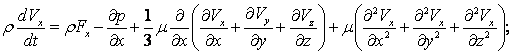
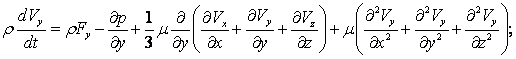
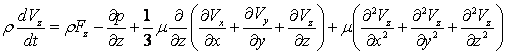В частном случае для несжимаемой жидкости () уравнение Навье-Стокса еще упрощается

или

(2.42)

Здесь коэффициент называется кинематической вязкостью.

Уравнение (2.42) вместе с уравнением неразрывности образует замкнутую систему уравнений Навье–Стокса для вязкой несжимаемой жидкости. Так же как и для идеальной жидкости, эта задача (механическая) решается отдельно от тепловой (см. п. 2.3.3).

Примечание.

Уравнения Навье–Стокса являются одними из важнейших в гидродинамике и применяются в численном моделировании многих природных явлений и технических задач. Но в аналитическом виде точные решения этих уравнений найдены лишь в некоторых частных случаях (течение в цилиндрической трубке круглого сечения под действием постоянной разности давлений (течение Пуазейля), течение между двумя параллельными стенками, одна из которых движется относительно другой (течение Куэтта) и др.), поэтому нет полного понимания свойств этих уравнений (например, при турбулентном течении (п. 2.5)).

Проблема существования и гладкости решений системы трехмерных уравнений Навье–Стокса является одной из семи математических «задач тысячелетия», сформулированных в 2000 г. Математическим институтом Клэя (США). За ее решение обещана премия $1 млн. Кстати, одна из этих задач – доказательство гипотезы Пуанкаре (топологическая проблема) уже решена в 2002 г. российским математиком Григорием Перельманом.

Конец примечания.