Рассмотрим адиабатическое движение идеальной жидкости.
Исключая ![]() из уравнения неразрывности
из уравнения неразрывности ![]() и уравнения изменения внутренней энергии
и уравнения изменения внутренней энергии ![]() , получим
, получим
![]()
или
![]() .
.
Отметим, что это же выражение можно получить из первого начала термодинамики (2.1), принимая во внимание адиабатичность процесса.
С другой стороны, если внутренняя энергия идеальной жидкости является функцией давления и времени![]() , то ее дифференциал
, то ее дифференциал
![]() .
.
Сравнивая оба выражения для ![]() , после преобразования получаем
, после преобразования получаем
|
|
(2.31) |
После интегрирования получаем зависимость вида ![]() , где C – константа, сохраняющая свое значение в движущейся жидкой частице.
, где C – константа, сохраняющая свое значение в движущейся жидкой частице.
Это уравнение связывает изменение давления с изменением плотности в движущейся частице жидкости, т.к. мы работали с полными производными ![]() и
и ![]() .
.
Жидкость называется баротропной, если ее плотность есть функция только давления: ![]() . В противном случае жидкость называется бароклинной.
. В противном случае жидкость называется бароклинной.
Таким образом, имеется баротропность для жидкой частицы.
Для установившихся течений имеется место баротропности для линии тока (т.к. траектории движения и линии тока в этом случае совпадают).
Рассмотрим частный случай: движение идеального газа.
В этом случае калорическое уравнение состояния
![]() , где
, где ![]() .
.
Тогда частные производные, входящие в уравнение (2.31), принимают вид
![]() ;
;![]() ,
,
а само уравнение преобразуется к простому виду
![]() .
.
После интегрирования получаем первый интеграл – уравнение адиабаты Пуассона
|
|
(2.32) |
При адиабатическом движении идеального газа отношение ![]() сохраняет постоянное значение. Параметр
сохраняет постоянное значение. Параметр ![]() называют показателем адиабаты.
называют показателем адиабаты.
Адиабату Пуассона ![]() и интеграл Бернулли
и интеграл Бернулли ![]() используют для расчета параметров установившегося адиабатического движения идеального газа вместо дифференциальных уравнений движения (Эйлера) и энергии.
используют для расчета параметров установившегося адиабатического движения идеального газа вместо дифференциальных уравнений движения (Эйлера) и энергии.
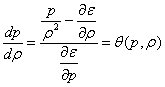 .
.