В силу многомерности и нелинейности уравнений движения идеальной жидкости их решение возможно только численными методами.

Но при определенных дополнительных допущениях некоторые из уравнений системы могут быть проинтегрированы. Эти допущения носят достаточно общий характер и выполняются во многих разных по характеру практических задачах. Полученные соотношения (их называют первыми интегралами системы уравнений) как уже отмечалось в первом разделе, более удобны для исследования задач, чем исходные уравнения.

Один такой интеграл – для потенциального течения несжимаемой идеальной жидкости мы получили – это интеграл Лагранжа–Коши.

Уберем условие несжимаемости и предположим, что:

• поле массовых сил потенциально, т.е. 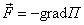, где П – потенциал поля;
• движение – установившееся (стационарное), т. е. .

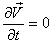Тогда уравнение Эйлера идеальной жидкости

с условием адиабатичности (2.3)

и замены (п.2.1.5)

примет вид

.

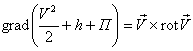При выводе интеграла Лагранжа–Коши (п. 2.3.4) нуль в правой части обеспечила потенциальность поля скоростей. Здесь же это не выполняется.

Можно, правда, указать частный случай, когда , следовательно, и – для всей области течения. Такое движение называется винтовым.

Но поступим по-другому: спроектируем это уравнение на направление касательное к линии тока. По определению линии тока это направление совпадает с направлением скорости, и проекция вектора на это направление будет равна нулю, т.к. (рис. 2.4).

Проекция же градиента на некоторое направление равна производной, взятой по этому направлению.

Поэтому

.

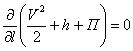Отсюда следует, что

вдоль линии тока.

(2.30)

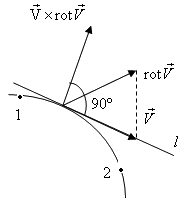Рис. 2.4. К выводу уравнения Бернулли

 

Это соотношение (первый интеграл уравнения Эйлера) называется интегралом Бернулли.

Интеграл Бернулли связывает параметры жидкости (при вышеупомянутых предположениях) в точках 1 и 2, находящихся на одной линии тока:

.

Частные случаи:

а) движение в поле сил тяжести ():

(сумма кинетической, тепловой и потенциальной энергии сохраняет свое постоянное значение на линии тока);

б) движение несжимаемой жидкости , тогда

и

.

Получили интеграл Лагранжа–Коши для стационарного течения. Отсюда вывод, что только в случае установившегося потенциального течения несжимаемой жидкости интеграл Бернулли переходит в интеграл Лагранжа–Коши и выполняется для любой точки пространства.

Этот интеграл показывает, что если пренебречь изменением потенциала сил (П=const)

,

то в потоке жидкости (с объявленными предположениями) существует однозначная зависимость между давлением и скоростью течения: повышение скорости всегда сопровождается уменьшением давления и наоборот;

в) движение несжимаемой жидкости в поле сил тяжести

(сохраняется сумма скоростной, пьезометрической и геометрической высот),

или в другом виде

(напор, или полное давление, равное сумме скоростного, гидростатического и высотного напоров, сохраняет свое постоянное значение);

г) движение совершенного газа (пренебрегаем изменением потенциала массовых сил и используем (2.25)):

или

,

где , – квадрат скорости звука в газе.

Отсюда следует: если газовый поток полностью затормозить, то энтальпия газа достигнет своего максимально возможного значения , называемого полной энтальпией, или энтальпией торможения. Соответствующая температура называется температурой торможения.

Этот интеграл показывает, что в потоке газа (с объявленными предположениями) существует однозначная зависимость между температурой газа (энтальпией) и скоростью течения: повышение скорости всегда сопровождается снижением температуры. При снижении скорости до нуля газ приобретает одинаковую температуру независимо от особенностей торможения.