Говорят, что уравнение в частных производных записано в «дивергентной форме», или, что эквивалентно, «в консервативной форме», если коэффициенты при производных являются константами. Обычно уравнения в частных производных, описывающие законы сохранения, записываются в дивергентной форме тогда, когда в них явно входит дивергенция той величины, для которой этот закон формулируется.

Например, уравнение неразрывности, описывающее закон сохранения массы (2.12)

,

записано в дивергентной форме (– поток плотности), а уравнение (2.11) – не в дивергентной форме.

Для дифференцируемых (неразрывных) решений эти уравнения эквивалентны. Однако во многих задачах МСС (например, в задачах газовой динамики) в поле течения образуются ударные волны – поверхности, на которых терпят разрыв параметры течения газа.

На поверхностях разрыва дифференциальные уравнения не имеют смысла, т.к. не существуют производные от разрывных функций. Поэтому при расчете течений с разрывами параметров необходимо пользоваться обобщенными решениями интегральных уравнений, описывающих законы сохранения («изменение какой-либо величины в некотором объеме равно потоку этой величины через поверхность этого объема»). Например, интегральное уравнение сохранения массы имеет вид

.

Эта форма полностью соответствует дивергентной форме записи дифференциального уравнения. Поэтому именно дивергентная форма правильно отражает физическую суть описываемого процесса.

Более того, из теории разностных схем численного решения дифференциальных уравнений известно, что и разностные схемы должны обладать тем же свойством (там оно называется консервативностью): консервативной схемой называются разностная схема, обеспечивающая точное выполнение законов сохранения (исключая погрешности округления) на любой сетке в конечной области, содержащей произвольное число узлов разностной сетки.

Уточним: любая согласованная разностная схема обеспечивает приближенное выполнение законов сохранения в большой области, но лишь консервативная разностная схема обеспечивает точное выполнение этих законов вследствие взаимного уничтожения ряда членов разностного уравнения (сокращаются все, кроме тех, которые описывают поток массы через границу). Если же используемая схема неконсервативна, то внутри области могут появиться источники и стоки небольшой интенсивности как артефакты разностного происхождения.

Запишем теперь два других уравнения – движения (2.16) и энергии (2.18) в дивергентном виде.

Преобразуем левую часть уравнения движения (2.16), перейдя от полной (субстанциональной) производной к частной производной и воспользовавшись уравнением неразрывности:

.

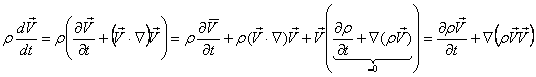Тогда уравнение движения примет вид

или

.

(2.22)

Здесь – тензор плотности потока импульса,

.

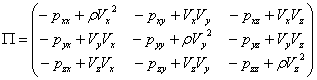Отметим, что этому уравнению (при ) соответствует интегральное уравнение сохранения импульса

.

Преобразуем и левую часть уравнения движения (2.18):

.

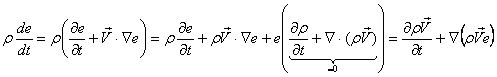Тогда уравнение энергии примет вид

или

.

(2.23)

При и этому уравнению соответствует интегральное уравнение сохранения энергии

.

В декартовых координатах система уравнений (2.12), (2.22), (2.23) запишется в виде

;

;

;

;

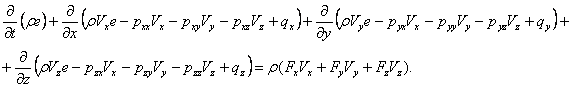
Вывод: для описания движения сплошной среды имеется пять скалярных дифференциальных уравнений в частных производных, представленных в дивергентном или недивергентном виде.

Сколько же неизвестных содержат эти уравнения? Подсчитаем, полагая, что внешние (массовые) силы известны:

• плотность ;
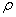• внутренняя энергия 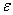(или полная энергия );
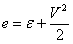• три компоненты вектора скорости ;
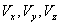• три компоненты вектора теплового потока ;
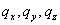• шесть компонентов тензора напряжений .

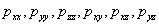Итого – 14 неизвестных.

Даже если предположить, что теплопередача происходит в соответствии с законом Фурье (тогда вместо трех переменных появится одна переменная Т – температура), то число неизвестных уменьшится только до 12.

Таким образом, система уравнений сплошной среды не замкнута (число уравнений меньше, чем число неизвестных).

Для разрешения проблемы замыкания необходимо использовать дополнительные предположения о свойствах сплошной среды, т.е. вводить модельные объекты сплошной среды.

Под модельным объектом сплошной среды понимают такую гипотетическую среду, в которой учтены только некоторые из физических свойств, существенные для определенного круга явлений и технических задач. Другие малосущественные свойства среды игнорируются.

Рассмотрим несколько широко используемых моделей: идеальная жидкость, идеальный газ, несжимаемая жидкость, вязкая ньютоновская жидкость.