Это уравнение описывает изменение импульса (количества движения) в сплошной среде.

Выделим в сплошной среде некоторый объем W и рассмотрим, какие силы влияют на его движение.

Во-первых, внешние, массовые силы (например, силы тяжести, электромагнитные силы, если движение происходит в электромагнитном поле).

Обозначим – массовую силу, действующую на единицу массы, тогда на весь рассматриваемый объем действуют силы

.

Во-вторых, внутренние (поверхностные) силы, возникающие при деформации этого объема под воздействием частиц жидкости, примыкающих к поверхности с внешней от выделенного объема стороны (силы вязкости, давления). Для их характеристики вводят понятие механического напряжения.

Выделим на поверхности объема W элемент . Пусть – равнодействующая всех сил воздействия на элемент поверхности . Тогда – вектор напряжения в точке А, принадлежащей площадке с нормалью , и

.

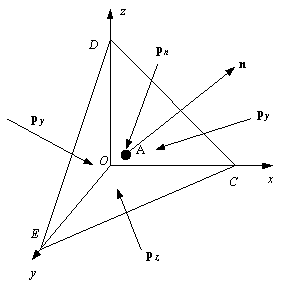
Рис. 2.3. Равновесие элементарного тетраэдра (к формуле Коши)

Но через точку можно провести множество плоскостей (элементарных площадок), поэтому напряжение – не простой вектор, он не является однозначной функцией координат и времени, зависит от ориентации нормали:  и, следовательно, не является полеобразующей величиной. К нему нельзя, например, применить формулу Остроградского–Гаусса.

Найдем, как напряжение в точке зависит от направления нормали.

Рассмотрим элементарный тетраэдр OCED, три грани которого параллельны координатным плоскостям, а четвёртая ориентирована произвольным образом (рис. 2.3). Обозначим – площадь этой четвертой грани.

Ориентация этой площади определяется нормалью где – направляющие косинусы (косинусы угла наклона единичной нормали к координатным осям).

Тогда

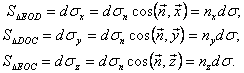
Объем тетраэдра равен , где h – высота тетраэдра, опущенная из вершины О на .

Если размеры тетраэдра достаточно малы, то можно считать, что напряжения, действующие на его гранях , ,,, постоянны в пределах каждой грани.

Применим теорему об изменении импульса (2-й закон Ньютона) к объему этого тетраэдра, заменив интегралы их средними значениями:

.

.

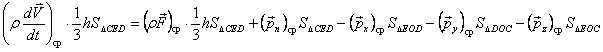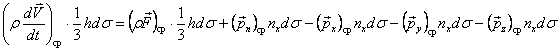Устремим , стягивая тетраэдр в точку. Предельный переход дает соотношение

,

т.е. напряжения на гранях образуют систему взаимно уравновешенных напряжений.

Получили формулу, позволяющую по положению нормали к плоскости вычислить действующее в этой плоскости напряжение (формула Коши условия равновесия бесконечно малого тетраэдра).

Проектируя на координатные оси, получаем три скалярных соотношения:

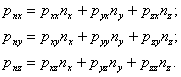
Коэффициенты при направляющих косинусах образуют тензор, который называется тензором напряжения. В декартовой системе координат координаты тензора напряжения имеют простой физический смысл: они равны нормальным и касательным напряжениям в соответствующих координатных площадках.

Таким образом, напряжение в произвольной точке сплошной среды определяется девятью скалярными величинами, образующими тензор напряжений:

,

(2.14)

и тогда

.

(2.15)

Этот тензор является полеобразующей величиной.

Теперь, используя лагранжев подход, запишем изменение импульса для произвольного объема среды W, которое равно главному вектору сил, действующих на тело:

.

Используя формулу дифференцирования объемного интеграла и теорему Остроградского–Гаусса, имеем:

.

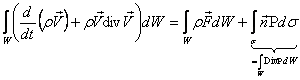Переходя от интегральной к дифференциальной форме уравнения, получаем

.

Преобразуем, выделив в нем левую часть уравнения неразрывности

.

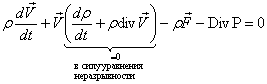Окончательно получаем уравнение движения в напряжениях:

,

(2.16)

где .
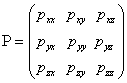