Полученное выражение (1.60) имеет понятный физический смысл: каково бы ни было внешнее воздействие на систему во время движения, ее конечное состояние не может быть произвольной функцией начального состояния – возможно только такое движение, при котором выражение, стоящее в правой части (1.60), является полным дифференциалом.

Воспользуемся этим выражением и принципом наименьшего действия, чтобы другим способом получить канонические уравнения Гамильтона. Ограничимся пока одной координатой.

Из (1.60) следует

.

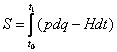Тогда

В силу независимости и

;  .

Таким образом, получены канонические уравнения Гамильтона для одной степени свободы:

; .

В общем случае

; .