Каждая система материальных точек описывается своей функцией Гамильтона ![]() . Вид функций Гамильтона определяет фазовые траектории, которые заполняют фазовое пространство. Какая именно фазовая траектория будет реализована, зависит от начальных условий. Движение по фазовым траекториям удовлетворяет принципу наименьшего действия:
. Вид функций Гамильтона определяет фазовые траектории, которые заполняют фазовое пространство. Какая именно фазовая траектория будет реализована, зависит от начальных условий. Движение по фазовым траекториям удовлетворяет принципу наименьшего действия: ![]() .
.
Но на каждой траектории значения экстремума действия будут различны. Поэтому можно рассматривать действие как величину, характеризующую движение по истинным траекториям.
Если сравнивать значения, которые действие имеет для траекторий, выходящих из общего начала ![]() , но проходящих в момент
, но проходящих в момент ![]() через различные положения, то действие для истинных траекторий будет являться явной функцией значений координат в верхнем пределе интегрирования
через различные положения, то действие для истинных траекторий будет являться явной функцией значений координат в верхнем пределе интегрирования ![]() .
.
Если рассматривать траектории, выходящие из общего начала ![]() , но заканчивающиеся в заданном положении
, но заканчивающиеся в заданном положении ![]() в различные моменты времени, то действие для истинных траекторий будет являться явной функцией времени.
в различные моменты времени, то действие для истинных траекторий будет являться явной функцией времени.
Таким образом, действие для истинных траекторий будет являться явной функцией и времени и координат: ![]() .
.
Попробуем, не зная конкретного вида этой функции, записать выражение для ее частных производных по времени и координатам ![]() и
и ![]() .
.
По определению действия его полная производная по времени вдоль траектории равна ![]() . Выражая L через гамильтониан:
. Выражая L через гамильтониан: ![]() , запишем дифференциал действия в виде
, запишем дифференциал действия в виде
|
|
(1.60) |
С другой стороны, дифференциал действия как функции координат и времени можно записать в виде
![]() .
.
Приравнивая правые части этих выражений, имеем
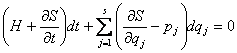 .
.
В силу независимости переменных имеем
|
|
(1.61) |
Эти соотношения ниже будут использованы для получения уравнения Гамильтона–Якоби.