Рассмотрим механическую систему, состоящую из N материальных точек и ограниченную l идеальными голономными связями.

Для описания ее движения можно использовать или непосредственно уравнения, которые дает II закон Ньютона, или основные теоремы динамики.

В первом случае записывается 3N уравнений:

;

;

,  (k=1…N).

Неизвестных здесь 6N (3N координат и 3N проекций реакций связи), поэтому вторая задача динамики в общем случае неразрешима.

Второй путь требует применения каждый раз разных теорем и для сложных систем приводит к большим математическим трудностям (т.е. нет универсального подхода).

Попробуем решить эти проблемы в обобщенных координатах. Определим положение системы в пространстве конфигураций s обобщенными координатами q_j.

Возьмем за основу общее уравнение динамики (принцип Даламбера – Лагранжа) и запишем его в обобщенных координатах.

или .

Левая часть уравнения – работа активных сил:

.

Правая часть уравнения – работа даламберовых сил инерции:

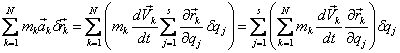
(изменить порядок суммирования можно в связи с независимостью суммирования по k и по j).

Выделим в последнем выражении отдельно сумму по k:

…

Преобразуем подчеркнутые сомножители: 1) ; 2) используем выражение (1.36): . Беря частную производную по , получаем . Продолжаем преобразование

….

Таким образом, общее уравнение динамики запишется в виде:

или

.

В силу произвольности виртуальных перемещений

(j=1,…,s).

(1.43)

Это и есть уравнения Лагранжа II рода – уравнения движения голономных систем в обобщенных координатах.

Характеристика этих уравнений:

1. Они образуют систему s дифференциальных уравнений второго порядка относительно sпеременных .

2. Их форма не зависит от выбора обобщенных координат . При другом их выборе изменятся только функции Т и Q_j, а сама форма уравнений осталась бы той же. В связи с этим говорят, что уравнения Лагранжа II рода обладают свойством ковариантности.

3. Они не содержат реакций идеальных связей. Это означает, что при использовании обобщенных координат удается отделить задачу нахождения закона движения несвободной системы от задачи определения неизвестных реакций связи.

Если же нужно найти эти реакции, то после интегрирования уравнений Лагранжа следует подставить найденные в выражение

,

и тогда равнодействующая реакций связи, приложенных к точке , найдется из принципа Даламбера:

.

4.   Уравнения Лагранжа позволяют указать единую последовательность действий, которые нужно выполнить при решении любой задачи динамики:

а) определить число степеней свободы;

б) выбрать обобщенные координаты;

в) записать кинетическую энергию системы, найти производные и ;

г) найти обобщенные силы; для этого:

-     изобразить на чертеже все приложенные силы, совершающие работу;

-     сообщить системе виртуальное перемещение, при котором меняется только координата q₁, и вычислить сумму элементарных работ всех действующих сил. Коэффициент при даст искомую силу Q₁;

-     аналогично вычислить Q₂, Q₃,…,Q_s;

д) составить уравнения движения и проинтегрировать их с учетом начальных условий.

В частном случае при движении под действием потенциальных сил

,

и уравнения Лагранжа примут вид

.

Так как потенциальная энергия является функцией обобщенных координат, времени, но не скоростей , то это уравнение можно формально представить в виде

или

(1.44)

(уравнение Лагранжа II рода для потенциальных сил).

Функция называется функцией Лагранжа (лагранжиан, кинетический потенциал). Совокупность переменных называется переменными Лагранжа.

Отметим особенность этих уравнений: если, например, какая-то из обобщенных координат j=i не входит явно в выражение для лагранжиана L, то и получаем первый интеграл уравнения в виде

, или .

Такие координаты q_i называются циклическими координатами.

Понятие функции Лагранжа распространяется и на системы с бесконечным числом степеней свободы – классические физические поля (электромагнитные, гравитационные, поля ядерных сил, квантованные (волновые) поля); при этом обобщенные координаты – значения функций поля. Соответственно, для них справедливы уравнения Лагранжа в виде (1.44).
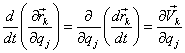