Пусть на систему N материальных точек наложено l голономных связей.

Число независимых виртуальных перемещений системы называется ее числом степеней свободы s. Это число определяется количеством независимых координат, однозначно определяющих положение материальной системы в пространстве. Очевидно, .

Примеры.

1) свободная точка в пространстве: s=3 (в качестве обобщенных координат выбираются декартовы координаты x,y,z);

2) точка на плоскости: s=2 (обобщенные координаты – плоские декартовы координаты x,y);

3) точка на кривой: s=1 (обобщенная координата – s– дуга траектории);

4) свободное движение твердого тела. Соединяем три любые точки А, В, С тела прямыми линиями, имеем девять неизвестных, определяющих координаты векторов , и три уравнения связи: s=6 (обобщенные координаты – x_р,y_р,z_ри 3 угла);

5) система из двух точек А и В, соединенных стержнем, движущаяся в плоскости, имеем 4 координаты точек и одно уравнение связи: s=3 (обобщенные координаты – две декартовы координаты точки А и угол между горизонталью и стержнем).

Эти независимые координаты не обязательно должны быть декартовыми. В зависимости от условий задачи может оказаться более удобным выбор каких-нибудь других координат, имеющих любую размерность и любой геометрический (или физический) смысл – дуга, угол, площадь и т.п. Поэтому их назвали  обобщенными.

Итак, обобщенными координатами называется совокупность независимых параметров , однозначно определяющих положение материальной системы в пространстве.

Требования к ним:

1) независимость;

2) должны однозначно определять положение системы в пространстве;

3) декартовы координаты x_k, y_k, z_kточек системы можно выразить через обобщенные, тогда радиус-вектор любой точки системы можно записать в виде

;

(1.35)

4) координаты выбираются в соответствии с уравнениями связей, т.е. функции должны обращать в тождество уравнения связей: , .

Для каждого момента времени между возможными положениями системы и точками s-мерного пространства устанавливается взаимно однозначное соответствие.

Пространство называется координатным пространством (или пространством конфигураций).

Каждому возможному положению системы отвечает некоторая точка координатного пространства – изображающая точка. Движению системы соответствует движение изображающей точки в координатном пространстве.

, , …, – кинематические уравнения движения в обобщенных координатах.

По аналогии с обычным понятием скорости и ускорения вводят понятие обобщенной скорости и обобщенного ускорения:

; ,    j=1…s.

Размерность обобщенной скорости и ускорения зависит от размерности соответствующей обобщенной координаты (если q – линейная величина, то – линейная скорость, если q– угол, то – угловая скорость, если q– площадь, то – секторная скорость и т.п.).

Связь скоростей и ускорений точек системы в декартовой системе координат и в пространстве конфигураций можно найти, продифференцировав (1.35).

; .

(1.36)

Для голономных связей обобщенные скорости независимы и совершенно произвольны (т.к. нет ограничений связи на скорости).

Связь виртуальных перемещений точек системы с вариациями обобщенных координат дается выражением

.

(1.37)

Эта формула справедлива и для любой функции :

.

Теперь определим понятие обобщенной силы.

По определению виртуальная работа всех сил, приложенных к точкам системы:

.

Заменим виртуальные перемещения через вариации обобщенных координат, тогда

.

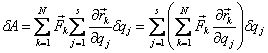Введем обозначение:

(j=1…s).

(1.38)

Тогда .

Величина Q_j называется обобщенной силой, соответствующей обобщенной координате .

Таким образом, обобщенные силы являются коэффициентами при вариациях обобщенных координат в выражении элементарной работы сил, действующих на материальную систему.

В практических задачах для вычисления обобщенных сил формулами (1.38) обычно не пользуются. Обычно дают системе такое виртуальное перемещение, при котором (i=1…s) для всех i, кроме i=j. Тогда

и

.

(1.39)

Перебирая все j, находим все Q_j .

Размерность обобщенной силы равна размерности работы, деленной на размерность соответствующей обобщенной координаты. Если q – линейная величина, то Q – это сила в обычном смысле, если q – угол поворота, то это момент силы относительно оси вращения, если q – объем, то Q – это давление и т.п.

В общем случае обобщенные силы будут функциями обобщенных координат, скоростей и времени.

Если же действующие силы потенциальные с потенциалом , тогда и обобщенные силы – потенциальные, причем им соответствует потенциал, полученный из функции , если в ней величины выразить через обобщенные координаты.

Получим выражение для потенциальных обобщенных сил.

В п.1.2.5.8 было получено соотношение , выполняющееся в поле стационарных потенциальных сил. Тогда соотношение будет выполняться и для нестационарного потенциального поля (вариация – изохронная). В этом соотношении

, .

Отсюда следует, что

.

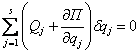В силу независимости вариаций обобщенных координат

(j=1…s).

(1.40)

Запишем основное уравнение статики в обобщенных координатах.

Принцип виртуальных перемещений гласит, что при равновесии системы или

.

В силу независимости вариаций обобщенных координат

Qj =0 (j=1…s).

(1.41)

Таким образом, можно сформулировать принцип Лагранжа в обобщенных координатах: для равновесия механической системы с идеальными голономными связями необходимо и достаточно, чтобы все обобщенные силы, соответствующие выбранным для системы обобщенным координатам, были равны нулю.

Число условий равновесия будет равно числу обобщенных координат, т.е. числу степеней свободы системы.

В частном случае, если все активные силы потенциальны, то условие равновесия

(j=1…s).

(1.42)

Вывод: необходимые и достаточные условия равновесия голономной системы (с идеальными удерживающими связями, в потенциальном поле сил) совпадают с необходимыми условиями экстремума потенциальной энергии в рассматриваемом положении равновесия системы.

Если , то условие равновесия принимает вид .