Введем понятия «действительное (истинное) перемещение», «возможное перемещение», «виртуальное перемещение» (на примере одной точки, подчиненной одной голономной удерживающей связи ).

Действительным перемещением точки называется бесконечно малое перемещение этой точки под действием как заданных сил, так и реакций связи; действительное перемещение происходит за время dtв соответствии с уравнением движения и уравнением связи: .

Возможным перемещением называют «перемещение» точки, допускаемое связью; в отличие от действительных перемещений возможное перемещение удовлетворяет только уравнению связи. Воображаемых перемещений – бесконечное множество. Действительное перемещение является одним из возможных.

Возможные перемещения подчиняются дифференциальному уравнению, которое получается, если продифференцировать уравнение связи

.

(1.28)

Виртуальным перемещением называется воображаемое бесконечно малое «перемещение» точки, допускаемое связью в данной фиксированный момент времени.

В этот момент времени связь «застывает», т.е. ее изменение со временем мысленно прекращается. Виртуальные перемещения не происходят под действием сил и не обладают длительностью.

Другими словами, виртуальное перемещение – это изохронная вариация радиуса-вектора точки, подчиненная уравнениям связи.

Примечание. О вариации.

Пусть – некоторая функция. Тогда главная линейная часть изменения функции, возникающего вследствие приращения аргумента на величину , называется дифференциалом функции

.

Наряду с этим можно рассматривать другое изменение функции, возникающее вследствие очень малого изменения самого вида функциональной зависимости и рассматриваемое при неизменном значении аргумента. Такое изменение называется вариацией функции.

Если записать

,

где – малое число, – любая дифференциальная функция,

то

и будет вариацией функции r(при неизменном t).

Конец примечания

Дифференциальное уравнение, которому подчиняется виртуальное перемещение точки, получим, вычисляя вариацию

.

(1.29)

Сравнивая (1.28) и (1.29), видим, что для стационарных связей возможные и виртуальные перемещения совпадают.

Обобщим уравнения (1.28) и (1.29) на систему N точек, подчиненных голономным удерживающим связям :

		(1.30)
		(1.31)

Пользуясь понятием виртуальных перемещений, дадим более широкое определение идеальных связей, понятие о которых мы ввели ранее.

Идеальными называются связи, сумма элементарных работ реакций которых на любом виртуальном перемещении точек системы равна нулю (иными словами – виртуальная работа реакций связей равна нулю):

(1.32)

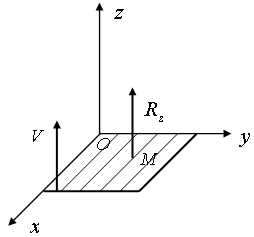Рис. 1.11. Идеальная связь

Пример. Точка М движется по абсолютно гладкой горизонтальной поверхности (рис. 1.11).

Тогда , следовательно, виртуальная работа т.к. для рассматриваемой связи – независимо от того, движется плоскость или покоится.

Отметим, что действительная работа совершаемая реакцией на действительном перемещении, если плоскость движется со скоростью V, будет отлична от нуля

.

Таким образом, виртуальная работа отражает физическое свойство поверхности – ее гладкость.

Сформулируем принцип виртуальных перемещений (принцип Лагранжа).

Для равновесия системы материальных точек, подчиненных удерживающим идеальным связям, необходимо и достаточно, чтобы равнялась нулю сумма элементарных работ активных сил на любом виртуальном перемещении системы из рассматриваемого положения равновесия, при условии, если в начальный момент система неподвижна:

(1.33)

или

.

Пользуясь уже известными положениями (принципами) механики Ньютона, этот принцип можно доказать, т.е. можно рассматривать его как теорему.

Доказательство.

Необходимость.

Если система находится в равновесии, то .

Сообщим системе виртуальное перемещение , тогда  .

Суммируя, имеем: или .

Так как связи идеальны: , то .

Достаточность (для стационарных связей).

Пусть выполняется соотношение .

Докажем от противного. Пусть система пришла в движение. Действительные перемещения входят в число виртуальных (если связи стационарны). Тогда по теореме об изменении кинетической энергии

,

где – возможные перемещения, с которыми совпадают действительные перемещения точек системы.

Это противоречит условию.

Теорема доказана.

Принцип виртуальных перемещений представляет собой самый общий принцип аналитической статики. Из него можно получить условия равновесия любой конкретной механической системы, т.е. он дает общее уравнение статики.

Примечание.

Если не все связи являются идеальными, например имеются связи с трением, то к активным силам следует добавить силы реакций, соответствующих неидеальным связям.

Конец примечания