Моментом импульса (моментом количества движения, кинетическим моментом) материальной точки относительно некоторой точки О пространства (которое может и не совпадать с какой-либо материальной точкой системы) называется вектор (рис. 1.7)

.

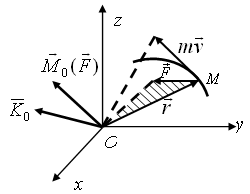Рис. 1.7.  К понятию момента импульса

Главным моментом импульса системы относительно центра О называется величина

.

Если импульс системы является характеристикой ее поступательного движения, то момент импульса является характеристикой вращательного движения.

Проиллюстрируем это на примере твердого тела, вращающегося вокруг неподвижной оси Oz. Для любой точки тела , где – расстояние от оси вращения, – угловая скорость вращения.

Тогда для этой точки

и ,

где – момент инерции тела относительно оси Oz.

Сравним: импульс равен произведению массы (величина, характеризующая инертность тела при поступательном движении) на линейную скорость: момент импульса равен произведению момента инерции (величина, характеризующая инертность тела при вращательном движении) на угловую скорость: .

Теорема.

Производная по времени от момента импульса системы относительно неподвижного центра равна главному моменту внешних сил системы относительно этого центра.

(1.8)

Покажем это.

Следствие этой теоремы – закон сохранения момента импульса: при движении замкнутой системы ее момент импульса относительно любого неподвижного центра постоянен:

при ,

(1.9)

или в проекциях на координатные оси

, .

Естественно, это утверждение справедливо не только для замкнутой системы, но и тогда, когда система не замкнута, но для некоторого неподвижного центра О во все время движения момент внешних сил (например, когда внешние силы центральные, т.е. ).

Предположим теперь, что точка (назовем ее Р), относительно которой рассматривается момент импульса, движется (рис. 1.8).

Тогда момент импульса системы запишется в виде

и, учитывая, что ,

получаем

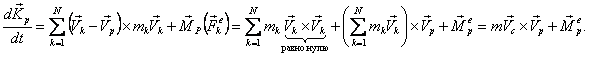
Производная по времени от момента импульса системы относительно подвижного центра равна сумме главного момента внешних сил системы относительно этого центра и векторного произведения импульса системы на скорость центра:

.

(1.10)

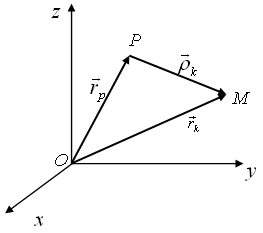Рис. 1.8. Момент импульса относительно подвижного центра

В этом случае для существования первого интеграла необходимо сделать дополнительные предположения.

Первый интеграл для замкнутой системы относительно подвижного центра

существует, когда радиусы-векторы и центра Р и центра масс системы С относительно начала координат О связаны отношением

,

где скалярная величина и вектор являются постоянными величинами.

Действительно, тогда , и первое слагаемое в правой части формулы (1.10) тождественно равно нулю.

При – случай неподвижного центра

При и , и формула (1.10) принимает вид

.

(1.11)

Таким образом, математические формулировки теоремы об изменении момента импульса системы для неподвижного центра О и для центра масс С имеют одинаковый вид.

 

Примеры.

1. Система, вращающаяся вокруг неподвижной оси (или проходящей через центр масс).

Тогда , и если , то .

Выводы:

а) если система – абсолютно твердое тело, то и, следовательно, , т.е. твердое тело, закрепленное на оси, будет вращаться с постоянной угловой скоростью;

б) если система изменяема, то действие внутренних сил может изменить угловую скорость вращения системы: при удалении точек от оси увеличивается и, следовательно, уменьшается и наоборот.

2. Кошка. При ее падении внешней силой является сила тяжести, которая не создает момента относительно центра тяжести кошки (система движется поступательно). Если момент был равен нулю в начале движения, то останется равным нулю и далее. Оказывается, кошка, усиленно вращая во время падения головой и хвостом, поворачивает свое тело в противоположную сторону на необходимый угол и приземляется на ноги. То же самое можно сказать об акробатах, балеринах, фигуристах, гимнастах (увеличение скорости вращения за счет уменьшения момента инерции).

3. Качели. Чтобы раскачаться, надо приседать в левом и правом верхних положениях, где угловая скорость (что очевидно не повлияет на величину ), а при прохождении вертикали резко выпрямляться. Центр масс приближается к оси вращения, уменьшается, возрастает.

4. Вертолет. До запуска двигателя момент импульса системы «корпус+винт+отбрасываемая масса воздуха» равен нулю. Силы взаимодействия между отдельными частями системы являются внутренними и не могут изменить этот момент. Поэтому корпус вертолета должен вращаться в противоположную сторону (реактивный момент).

Чтобы предотвратить реактивное вращение корпуса одновинтового вертолета, на его хвостовой части устанавливают рулевой винт. У многовинтового вертолета винты делают вращающимися в разные стороны.

 

Примечание.

Сохранение момента импульса связано с изотропией пространства, в силу которого механические свойства замкнутой системы не изменяются при любом повороте системы как целого.

Изотропия пространства приводит к инвариантности физических законов относительно вращений пространства.

Конец примечания.