8.2.1. Определение. Арифметическим пространством называется алгебраическая структура

,

где 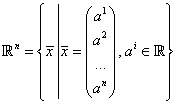, операции «+» и «•» определены так:  , . Данное пространство обозначается .

8.2.2. Теорема. Пространство есть n-мерное линейное пространство над полем .

8.2.3. Обозначение. Если матрица A имеет столбцами векторы арифметического пространства, то мы пишем .

8.2.4. Теорема. .

8.2.5. Теорема. Система векторов 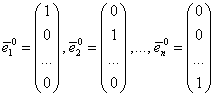составляет базис пространства .

Определение. Этот базис называется натуральным базисом.

8.2.6. Теорема. Векторы составляют базис пространства тогда и только тогда, когда .

8.2.7. Определение. Линейной 1-формой (ковектором) на линейном пространстве называется отображение

,

обладающее следующими свойствами:

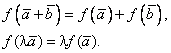
8.2.8. Определение суммы ковекторов и произведения ковектора на вещественное число.

8.2.9. Теорема. Если U – множество всех ковекторов на линейном пространстве , то структура есть n-мерное линейное пространство над полем .

Определение. Это линейное пространство называется сопряженным пространству .

8.2.10. Обозначение. Ковекторы обозначаем символами вида .

8.2.11. Теорема. Пусть – базис линейного пространства . Пусть – система ковекторов таких, что (символ Кронекера). Тогда есть базис сопряженного пространства.

Определение. Базис называется дуальным для базиса .

8.2.12. Теорема. Если , то .

8.2.13. Определение. Число называется скалярным произведением ковектора и вектора и обозначается любым из следующих способов: , .

8.2.14. Теорема. Если базис пространства преобразуется по формуле , то дуальный базис преобразуется так: .

8.2.15. Поскольку отождествляется со столбцом и , то ковектор естественно отождествлять с вектором-строкой, а линейное пространство, сопряженное пространству , отождествить с линейным пространством векторов-строк , отличие которого от заключается только в форме записи вектора. Мы получаем еще одно линейное пространство .

8.2.16. Теорема Всякое n-мерное линейное пространство над изоморфно линейному пространству .

Следствие. Мы ничего не потеряем в общности наших построений, если под линейным пространством будем подразумевать арифметическое пространство.