Напомним,что сопряжённый оператор ![]() к оператору
к оператору ![]() , где
, где ![]() – гильбертовы пространства, задаётся равенством
– гильбертовы пространства, задаётся равенством ![]() . (1) Равенство (1), что важно, выполняется при любых
. (1) Равенство (1), что важно, выполняется при любых ![]() .
.
Часто рассматривается случай ![]() , но это необязательно.
, но это необязательно.
Пример 1. Оператор замены переменной.
Найти сопряжённый к оператору ![]() .
.
Имеем ![]() . Воспользуемся равенством (1) (справа налево):
. Воспользуемся равенством (1) (справа налево):
 , (2)
, (2)
Заменяя в (2), в первом интеграле в правой части ![]() на
на ![]() , получим:
, получим:  Таким образом,
Таким образом,  .Следовательно,
.Следовательно, ![]() . Полученное равенство выполняется при всех
. Полученное равенство выполняется при всех ![]() , то есть вектор
, то есть вектор ![]() ортогонален всему пространству
ортогонален всему пространству ![]() . Поэтому он равен 0, откуда
. Поэтому он равен 0, откуда ![]() .
.
Пример 2. Оператор умножения на функцию.
Найти сопряжённый к оператору![]() .
.
Применим ту же схему рассуждений, что и в предыдущем примере.  . Из последнего равенства, так же как и в примере 1, выводится, что
. Из последнего равенства, так же как и в примере 1, выводится, что ![]() .
.
Пример 3. Оператор сдвига.
Найти сопряжённый к оператору  .
.
Аргументы, применявшиеся в примере 1, сохраняют силу и здесь. Проделаем только вычисления, основанные на равенстве (1). 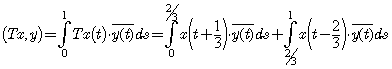 . Полагая в первом из получившихся интегралов
. Полагая в первом из получившихся интегралов ![]() , а во втором
, а во втором ![]() , получим:
, получим:  . Это равенство показывает, что
. Это равенство показывает, что  .
.
Пример 4. Оператор Фредгольма.
Найти сопряжённый к оператору  .
.
Из курса лекций известно, что сопряжённым к оператору Фредгольма с ядром ![]() является оператор Фредгольма с ядром
является оператор Фредгольма с ядром ![]() . Поэтому
. Поэтому  .
.
Пример 5.
Найти сопряжённый к оператору ![]() .
.
В нашем случае ![]() . Обозначим
. Обозначим ![]() . Равенство (1) запишется в виде
. Равенство (1) запишется в виде ![]() . (3)
. (3)
Напомним, что это равенство выполняется при любом ![]() . Это даёт возможность найти координаты вектора
. Это даёт возможность найти координаты вектора ![]() . А именно, будем по очереди подставлять в (3) вместо
. А именно, будем по очереди подставлять в (3) вместо ![]() векторы вида
векторы вида ![]() , где единица стоит на n-м месте. Тогда левая сумма в (3) будет равна
, где единица стоит на n-м месте. Тогда левая сумма в (3) будет равна ![]() , а правая будет равна
, а правая будет равна ![]() . При
. При ![]() получится, очевидно,
получится, очевидно, ![]() , а при
, а при ![]() получим
получим ![]() . Таким образом,
. Таким образом, ![]() .
.