Для линейного ограниченного функционала ![]() , определенного на линейном нормированном пространстве
, определенного на линейном нормированном пространстве ![]() , число
, число ![]() называется нормой функционала
называется нормой функционала ![]() .
.
Линейное пространство всех линейных ограниченных функционалов ![]() с такой нормой обозначается
с такой нормой обозначается ![]() и является банаховым пространством.
и является банаховым пространством.
Для того, чтобы доказать, что данное число ![]() является нормой функционала
является нормой функционала ![]() (т.е. является точной верхней границей множества значений этого функционала на единичном шаре
(т.е. является точной верхней границей множества значений этого функционала на единичном шаре ![]() ) нужно:
) нужно:
Доказать неравенство ![]() для всех
для всех ![]() . Это будет означать, что число
. Это будет означать, что число ![]() является верхней границей для множества
является верхней границей для множества ![]() и, следовательно,
и, следовательно, ![]() .
.
Найти последовательность элементов ![]() ,
, ![]() , таких, что
, таких, что ![]() , или найти один элемент
, или найти один элемент ![]() ,
, ![]() , для которого
, для которого ![]() . Это будет означать, что
. Это будет означать, что
![]()
или, в случае, когда удается найти один элемент,
![]() .
.
Задача 1. Докажите, что функционал ![]() , определенный формулой
, определенный формулой ![]() , является ограниченным, и найдите его норму.
, является ограниченным, и найдите его норму.
Решение. Для функции ![]() имеем
имеем
![]() .
.
Отсюда следует, что значения функционала ![]() на единичном шаре ограничены числом 3. Для функции
на единичном шаре ограничены числом 3. Для функции ![]() из единичного шара
из единичного шара ![]() ,
, ![]() и, следовательно,
и, следовательно, ![]() , только если
, только если ![]() и
и ![]() . Такой функцией является, например, функция
. Такой функцией является, например, функция
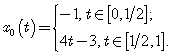

Задача 2. Докажите, что функционал ![]() , определенный формулой
, определенный формулой 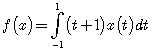 , является ограниченным, и найдите его норму.
, является ограниченным, и найдите его норму.
Решение. Пусть ![]() Тогда
Тогда
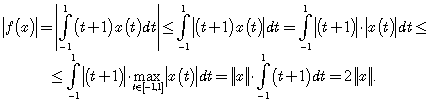 .
.
Отсюда следует, что ![]() . Кроме того, из этого неравенства видно, что самое большое значение, которое функционал может принять на единичном шаре, – это
. Кроме того, из этого неравенства видно, что самое большое значение, которое функционал может принять на единичном шаре, – это 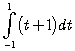 . Нетрудно видеть, что если
. Нетрудно видеть, что если ![]() , то
, то 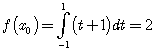 и, значит,
и, значит, ![]() . Окончательно получаем, что
. Окончательно получаем, что ![]() .
.
Задача 3. Докажите, что функционал ![]() , определенный формулой
, определенный формулой 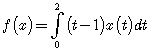 , является ограниченным, и найдите его норму.
, является ограниченным, и найдите его норму.
Решение. Пусть ![]() Тогда
Тогда
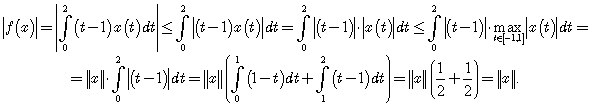 .
.
Отсюда следует, что ![]() Кроме того, из этого неравенства видно, что
Кроме того, из этого неравенства видно, что  , если
, если ![]() . Единственной функцией (с точностью до меры ноль), для которой
. Единственной функцией (с точностью до меры ноль), для которой ![]() и
и 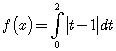 , является функция
, является функция
Функция ![]() является разрывной, т.е.
является разрывной, т.е. ![]() . Это означает, что на единичном шаре пространства
. Это означает, что на единичном шаре пространства ![]() функционал
функционал ![]() не принимает значение 1. Рассмотрим последовательность функций
не принимает значение 1. Рассмотрим последовательность функций ![]() , поточечно сходящихся к функции
, поточечно сходящихся к функции ![]() , таких, что
, таких, что ![]() для каждого
для каждого ![]() . Например,
. Например,
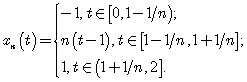
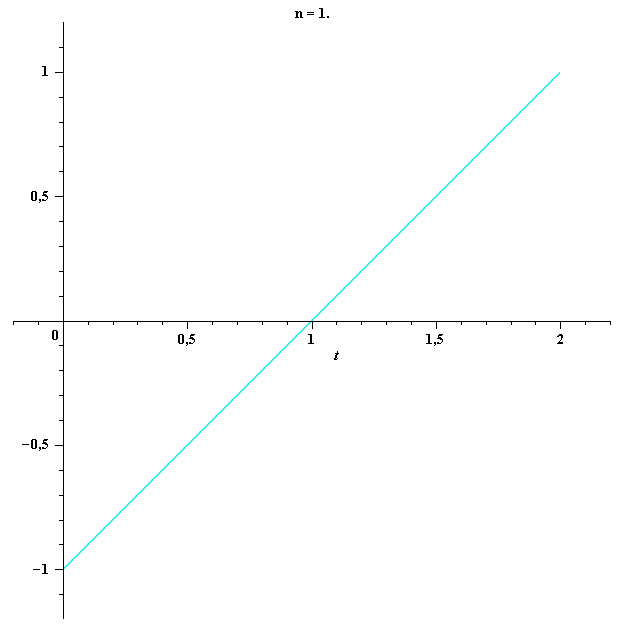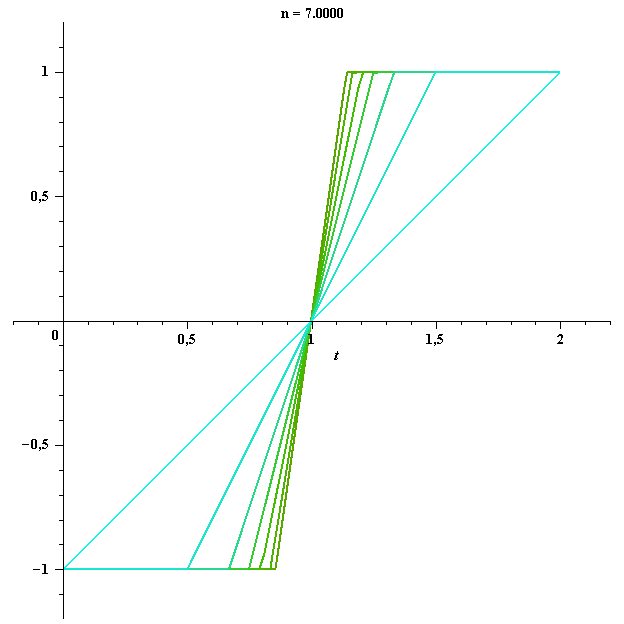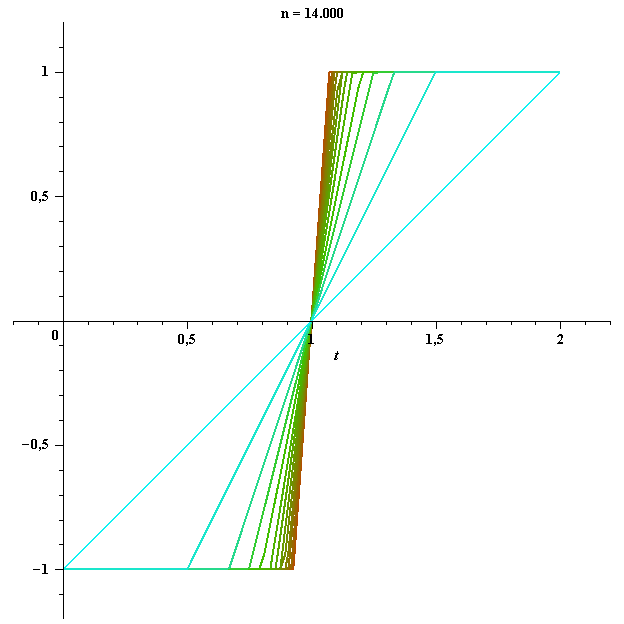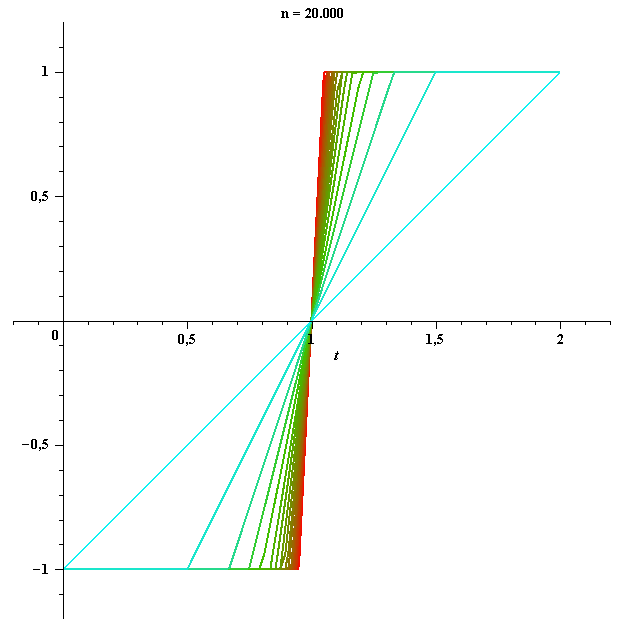
Тогда
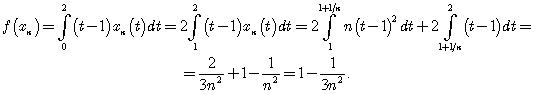
Таким образом, получили, что ![]() . Из двух полученных неравенств имеем, что
. Из двух полученных неравенств имеем, что ![]() .
.
Задача 4. Является ли ограниченным функционал ![]() , определенный формулой
, определенный формулой ![]() .
.
Решение. Данный функционал не определен на всем пространстве ![]() . Например, для непрерывной на отрезке
. Например, для непрерывной на отрезке ![]() функции
функции
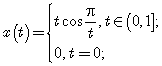
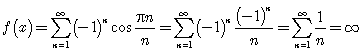 . Даже если мы рассмотрим данный функционал на области определения, т.е. на множестве
. Даже если мы рассмотрим данный функционал на области определения, т.е. на множестве ![]() , то на функциях
, то на функциях ![]() , где
, где ![]() – это ломаная, соединяющая точки
– это ломаная, соединяющая точки ![]() ,
,
значение функционала ![]() будет стремиться к бесконечности:
будет стремиться к бесконечности: ![]() . Это означает, что на
. Это означает, что на ![]() функционал
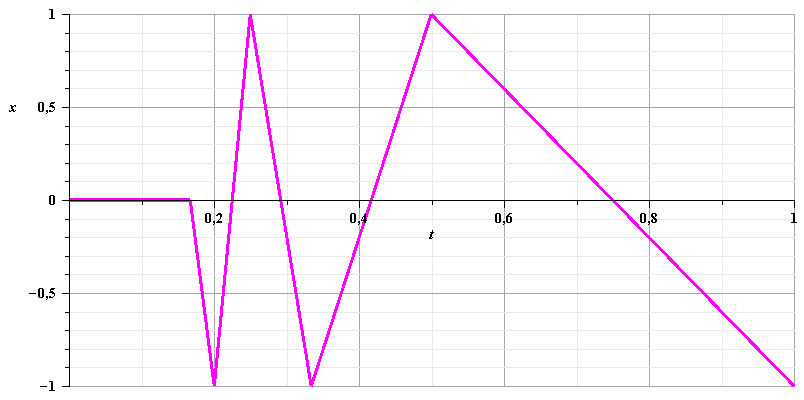
функционал ![]() является неограниченным. График функции
является неограниченным. График функции ![]() показан на рисунке:
показан на рисунке:
Задача 5. Докажите ограниченность функционала ![]() , заданного формулой
, заданного формулой 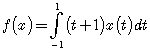 , и найдите его норму.
, и найдите его норму.
Решение. Для функции ![]() имеем
имеем
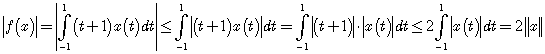 .
.
Таким образом, получили оценку ![]() . Заметим, что не существует такой функции, для которой почти для всех
. Заметим, что не существует такой функции, для которой почти для всех ![]() будет выполняться равенство
будет выполняться равенство ![]() , т.е. нет такой функции
, т.е. нет такой функции ![]() , что
, что ![]() и
и ![]() . Рассмотрим последовательность функций
. Рассмотрим последовательность функций ![]() ,
, ![]() , носители (носитель – это множество тех точек, в которых функция отлична от нуля) которых сосредоточены на полуинтервалах
, носители (носитель – это множество тех точек, в которых функция отлична от нуля) которых сосредоточены на полуинтервалах ![]() , т.е. в окрестности точки
, т.е. в окрестности точки ![]() , в которой функция
, в которой функция ![]() принимает наибольшее значение. Например,
принимает наибольшее значение. Например,
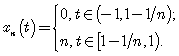
Тогда
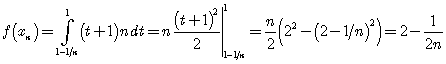 ,
,
откуда ![]() . Таким образом,
. Таким образом, ![]() .
.
Замечание. Если рассматривать функции ![]() , для которых
, для которых 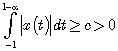 для некоторого
для некоторого ![]() и некоторого фиксированного
и некоторого фиксированного ![]() , то
, то
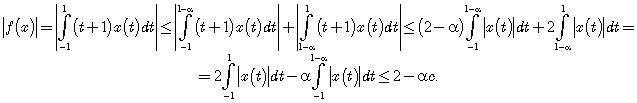
Отсюда следует, что среди таких функций мы не найдем последовательность ![]() , для которой бы
, для которой бы ![]() . Поэтому для любого
. Поэтому для любого ![]() необходимо рассматривать функции
необходимо рассматривать функции ![]() , которые равны нулю на промежутке
, которые равны нулю на промежутке ![]() . Одна из таких последовательностей и была взята при решении задачи.
. Одна из таких последовательностей и была взята при решении задачи.
Задача 6. Докажите ограниченность функционала ![]() , заданного формулой
, заданного формулой 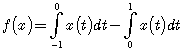 , и найдите его норму.
, и найдите его норму.
Решение. Для функции ![]() имеем
имеем
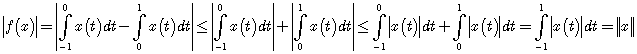
и, значит, ![]() .
.
Заметим, что данный функционал можно записать, как и в предыдущем примере, в виде 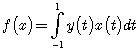 , где
, где ![]() Поскольку
Поскольку ![]() , то мы можем выбрать любую функцию
, то мы можем выбрать любую функцию ![]() ,
, ![]() , носитель которой содержится либо в интервале
, носитель которой содержится либо в интервале ![]() , либо в интервале
, либо в интервале ![]() . Для таких функций
. Для таких функций
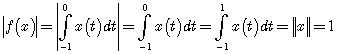 или, соответственно,
или, соответственно, 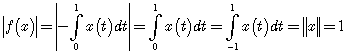 .
.
Таким образом, ![]() .
.
Задача 7. Докажите, что функционал ![]() , заданный формулой
, заданный формулой 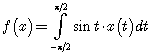 , ограничен, и найдите его норму.
, ограничен, и найдите его норму.
Решение. Пространство ![]() является гильбертовым пространством, и по теореме Рисса функционал
является гильбертовым пространством, и по теореме Рисса функционал 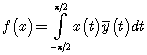 является ограниченным, если
является ограниченным, если ![]() . В нашей задаче
. В нашей задаче ![]() и, значит, функционал является ограниченным. Используя неравенство Коши–Буняковского, получаем
и, значит, функционал является ограниченным. Используя неравенство Коши–Буняковского, получаем
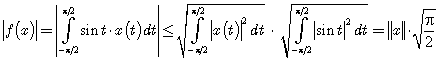 ,
,
т.е. ![]() .
.
Как показано в теореме Рисса, максимальное значение на единичном шаре непрерывный функционал принимает в точке ![]() . Следовательно, если мы рассмотрим функцию
. Следовательно, если мы рассмотрим функцию ![]() , то, во-первых,
, то, во-первых, ![]() , а во-вторых,
, а во-вторых, 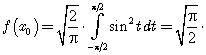 Таким образом,
Таким образом, ![]() .
.
Задача 8. Является ли ограниченным функционал 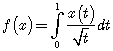 на своей области определения
на своей области определения ![]() ?
?
Решение. Данный функционал не определен на всем пространстве ![]() , так как, например, для функции
, так как, например, для функции 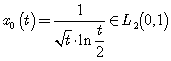 будет
будет
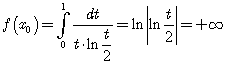 .
.
Рассмотрим функции 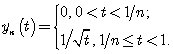 Вычислим их нормы:
Вычислим их нормы: 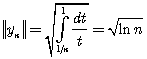 . Тогда для функций
. Тогда для функций ![]() имеем:
имеем: ![]() , а
, а 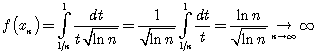 . Это означает, что функционал неограничен на своей области определения.
. Это означает, что функционал неограничен на своей области определения.
Для нахождения нормы функционалов ![]() нужно воспользоваться теоремами об общем виде функционалов на соответствующих пространствах. В доказательствах этих теорем приведены неравенства, необходимые для оценки значений
нужно воспользоваться теоремами об общем виде функционалов на соответствующих пространствах. В доказательствах этих теорем приведены неравенства, необходимые для оценки значений ![]() , и указаны элементы
, и указаны элементы ![]() , для которых
, для которых ![]() .
.