Пусть дана функция 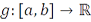. Ее вариационной суммой назовем выражение

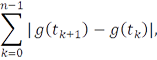
где 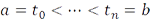– некоторое разбиение отрезка 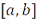. Выражение

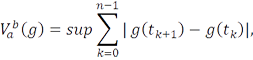
где супремум,  взятый по всем разбиениям отрезка 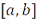,  называется вариацией функции 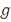на этом отрезке. Функция 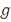называется функцией ограниченной вариации, если .

 

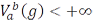Теорема 19.1. Линейная комбинация функций ограниченной вариации является функцией ограниченной вариации.

Следовательно,  множество всех функций ограниченной вариации на отрезке 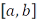является линейным пространством, которое обозначается символом 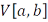. Это пространство содержит все монотонные функции, как показывает следующая теорема.

 

Теорема 19.2. Если функция 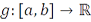монотонна, то 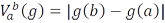. Следовательно, все монотонные функции являются функциями ограниченной вариации. В общем случае структура функций ограниченной вариации сводится к случаю монотонных функций.

 

Теорема 19.3 (Жордана). Если 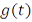– функция ограниченной вариации на отрезке 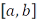, то существуют неубывающие функци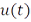и и 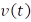такие, что .

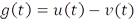Перейдем к определению интеграла Стилтьеса. Пусть заданы отрезок 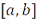и функция 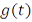ограниченной вариации на нем. Пусть, далее, 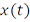– некоторая функция на отрезке 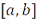. Сумму вида

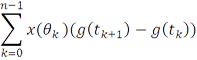
где 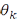– некоторая точка в промежутке 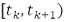, назовем интегральной суммой Стилтьеса. Если существует предел всех интегральных сумм Стилтьеса при условии, что длины промежутков разбиения стремятся к нулю и этот предел не зависит от выбора точек 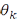, то этот предел называется интегралом Стилтьеса, который обозначается так:

 

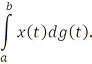
Теорема 19.4. Если 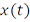–  непрерывная функция и 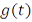–  функция ограниченной вариации на промежутке 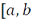], то интеграл Стилтьеса существует и конечен.

С помощью понятия интеграла Стилтьеса мы теперь можем сформулировать теорему об общем виде функционала на пространстве .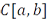

 

Теорема 19.5. Если 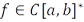– линейный ограниченный функционал, то существует функция ограниченной вариации 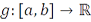такая, что

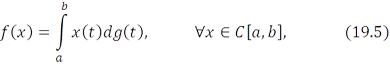
при чем

Верно и обратное: формула (19.1) определяет линейный функционал на пространстве 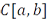, норма которого вычисляется по формуле (19.2).