Конечная или бесконечная система векторов 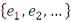называется ортогональной, если все векторы попарно ортогональны между собой. Она называется ортонормированной, если дополнительно выполнено условие: 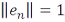для всех .

 

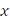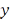Теорема Пифагора 10.1. Если вектора и ортогональны, то .

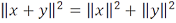Если система векторов 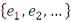ортонормирована и 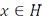, то выражение 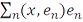называется рядом Фурье элемента 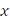по этой системе, а числа 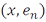– его коэффициентами Фурье.

 

 

Теорема 10.2 (Неравенство Бесселя). Для любой ортонормированной системы 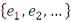и любого вектора 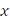в гильбертовом пространстве 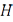выполнено неравенство

.

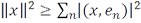Ортонормированная система называется полной, если к ней нельзя добавить ни одного ненулевого вектора с сохранением свойства ортогональности.

 

 

Теорема 10.3 (Равенство Парсеваля). Для полной ортонормированной системы 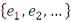и любого вектора 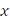в гильбертовом пространстве 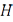выполнено равенство

.

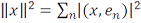Полные ортонормированные системы являются ортонормированными базисами. Это означает, что произвольный вектор 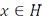разлагается в свой ряд Фурье, т.е. выполнено равенство

.

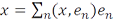Возникает вопрос: как строить ортонормированные базисы и в каких гильбертовых пространствах они существуют? Во-первых,  заметим, что пространства с ортонормированным базисом являются сепарабеотными пространствами. В самом деле, счетное всюду плотное подмножество в них образуют всевозможные конечные линейные комбинации векторов 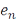с рациональными коэффициентами. Оказывается, что свойства сепарабельности гильбертова пространства достаточно для существования в нем ортонормированного базиса. Для доказательства этого факта нам понадобятся следующие определения.

1) Бесконечная система векторов называется линейно независимой, если любая конечная подсистема линейно независима.

2) Если 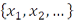– система векторов, то обозначим 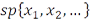совокупность всех конечных линейных комбинаций этой системы.

 

 

Теореме 10.4 (Ортогонализация по Шмидту). Пусть 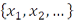– линейно независимая система векторов в гильбертовом пространстве. Тогда существует ортонормированная система 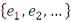такая, что 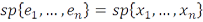для каждого .

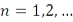Следовательно, если мы возьмем систему векторов 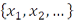, линейная оболочка которой всюду плотна, то методом ортогонализации мы получим ортонормированный базис в соответствующем гильбертовом пространстве.

 

Пример 10.5. Тригонометрическая система функций: 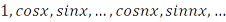образует ортогональный базис в 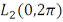. Каждая из систем: 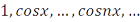и 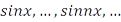будет образовывать ортогональный базис в пространстве .

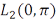Мы завершим этот параграф теоремой об общем виде функционала на гильбертовом пространстве.

 

Теорема 10.6  (Рисс). Если 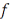– линейный ограниченный функционал на гильбертовом пространстве 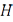, то существует единственное 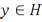такое, что 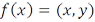для всех 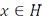, причем .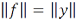