Множество называется относительно компактным, если его замыкание компактно.  Следующая теорема дает удобный способ проверки свойства относительной компактности в банаховых пространствах.

 

Теорема 8.1  (Хаусдорф). Множество 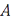в полном метрическом пространстве является относительно компактным тогда и только тогда, когда для каждого 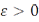существует конечная 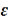–сеть, т.е. такое конечное множество точек 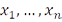, что любая точка в 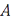отстоит от некоторой точки 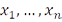на расстоянии, не большем .

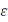Сформулируем критерий относительной компактности в пространстве .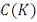

 

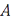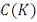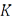Теорема 8.2  (Арцела–Асколи). Множество в пространстве , где – метрический компакт с метрикой 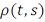,является относительно компактным тогда и только тогда, когда оно

1)      ограничено,

2)      равностепенно непрерывно (т.е. для каждого 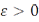существует 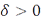такое, что из неравенства 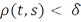следует для всех ).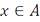

Дадим теперь главное определение данного параграфа.

 

Определение 8.3. Линейный оператор называется компактным или, по другой терминологии, вполне непрерывным, если он переводит ограниченные множества в относительно компактные.

 

 

Теорема 8.4. Линейный вполне непрерывный оператор является непрерывным.

Назовем линейный оператор 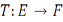конечномерным, если его образ 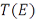является конечномерным подпространством в .

 

 

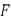Теорема 8.5. Конечномерный оператор является компактным.

 

 

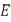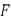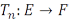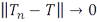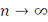Теорема 8.6. Пусть и – банаховы пространства. Если –последовательность вполне непрерывных операторов и при , то 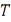– вполне непрерывный оператор.

Следовательно, множество всех компактных операторов образует замкнутое подмножество множества всех линейных огрниченных операторов. Из этих двух теорем следует, что операторы, которые аппроксимируются последовательностями конечномерных операторов, являются компактными. На протяжении примерно 50 лет стояла проблема Мазура: каждый ли компактный оператор аппроксимируется конечномерными? Эту проблему отрицательно решил шведский математик П. Энфло в 70-х годах ХХ века. В то же время в ряде случаев такая аппроксимация возможна. В частности, в следующей главе мы увидим, что в гильбертовых пространствах компактные операторы всегда аппроксимируются конечномерными операторами (см. теорему 12.5 ниже).

Приведем важные для дальнейшего примеры компактных операторов. Назовем оператор, заданный формулой

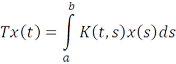- оператором Фредгольма. Здесь 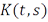– некоторая измеримая по Лебегу функция на квадрате , которую принято называть ядром оператора Фредгольма.Этот оператор можно рассматривать в разных пространствах функций. Приведем два утверждения про эти операторы.

 

 

Теорема 8.7. Пусть ядро 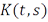является непрерывной функцией на квадрате . Тогда оператор Фредгольма, рассматриваемый как оператор 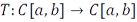, является компактным.

 

 

Теорема 8.8. Пусть ядро 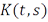является квадратично суммируемой функцией на квадрате , т.е. такой, что

.

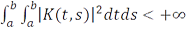Тогда оператор Фредгольма, рассматриваемый как оператор 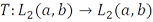, является компактным.