Множеству комплексных чисел ![]() ,
, ![]() ,
, ![]() , соответствует множество
, соответствует множество ![]() – комплексная плоскость
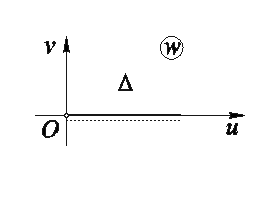
– комплексная плоскость ![]() с разрезом по лучу, идущему из нуля по положительной части действительной оси (рис. 12). Разрез имеет два края: верхний – на нем
с разрезом по лучу, идущему из нуля по положительной части действительной оси (рис. 12). Разрез имеет два края: верхний – на нем ![]() ,
, ![]() – и нижний – геометрически совпадающий с верхним краем, но исключаемый из рассмотрения условием
– и нижний – геометрически совпадающий с верхним краем, но исключаемый из рассмотрения условием ![]() .
.
Рисунок 12 (n=5)
Рисунок 13 (n=5)
Рисунок 14 (n=5)
Представим плоскость ![]() комплексного переменного
комплексного переменного ![]() как объединение
как объединение ![]() попарно непересекающихся множеств
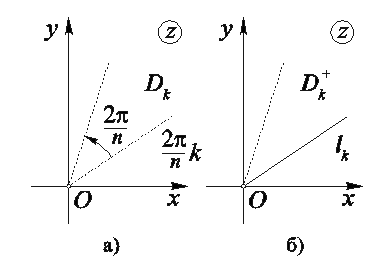
попарно непересекающихся множеств ![]() получающихся присоединением к угловой области
получающихся присоединением к угловой области ![]() луча
луча ![]() , входящего в границу области
, входящего в границу области ![]() (рис. 13). Объединение
(рис. 13). Объединение ![]() совпадает с
совпадает с ![]() . Каждая функция
. Каждая функция ![]() ,
, ![]() , однозначна на
, однозначна на ![]() -плоскости с разрезом, то есть на
-плоскости с разрезом, то есть на ![]() , и имеет значения, принадлежащие
, и имеет значения, принадлежащие ![]() и заполняющие это множество. Для преодоления неудобств, связанных с многозначностью
и заполняющие это множество. Для преодоления неудобств, связанных с многозначностью ![]() , поступим, воспроизводя идею Римана, следующим образом. Возьмем
, поступим, воспроизводя идею Римана, следующим образом. Возьмем ![]() комплексных плоскостей с разрезом
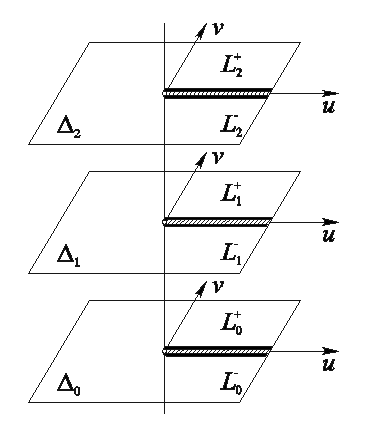
комплексных плоскостей с разрезом ![]() и будем считать, что они расположены друг над другом и получены сдвигом вверх по направлению, ортогональному плоскости
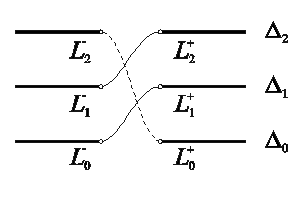
и будем считать, что они расположены друг над другом и получены сдвигом вверх по направлению, ортогональному плоскости ![]() (рис. 14). Соединим (склеим) нижний край разреза на
(рис. 14). Соединим (склеим) нижний край разреза на ![]() с верхним краем разреза на
с верхним краем разреза на ![]() , нижний край разреза на
, нижний край разреза на ![]() с верхним краем разреза на
с верхним краем разреза на ![]() и т.д. Наконец, соединим нижний край разреза на
и т.д. Наконец, соединим нижний край разреза на ![]() с верхним краем разреза на
с верхним краем разреза на ![]() (эта процедура не может быть проиллюстрирована построениями в
(эта процедура не может быть проиллюстрирована построениями в ![]() ) (рис. 15). Получается связная поверхность
) (рис. 15). Получается связная поверхность ![]() – поверхность Римана для
– поверхность Римана для ![]() , имеющая следующее свойство. Поднимем точку
, имеющая следующее свойство. Поднимем точку ![]() на плоскости
на плоскости ![]() . Будем перемещать точку
. Будем перемещать точку ![]() , взятую на
, взятую на ![]() , по непрерывной кривой, лежащей на
, по непрерывной кривой, лежащей на ![]() и не пересекающей линию склейки
и не пересекающей линию склейки ![]() с
с ![]() , в точку
, в точку ![]() на
на ![]() . Тогда значение
. Тогда значение ![]() непрерывно переместится в значение
непрерывно переместится в значение ![]() , причем
, причем ![]() . Читатель легко убедится, что подобным образом реализуется переход от
. Читатель легко убедится, что подобным образом реализуется переход от ![]() к
к ![]() . На поверхности
. На поверхности ![]() можно рассматривать
можно рассматривать ![]() -окрестности точки и распространить понятие непрерывности
-окрестности точки и распространить понятие непрерывности ![]() .
.
Рисунок 15 (n=5)
Таким образом, функция ![]()
![]() -значная на комплексной плоскости, становится однозначной на своей римановой поверхности. Точка
-значная на комплексной плоскости, становится однозначной на своей римановой поверхности. Точка ![]() является точкой ветвления римановой поверхности
является точкой ветвления римановой поверхности ![]() (точнее, алгебраической точкой ветвления порядка
(точнее, алгебраической точкой ветвления порядка ![]() ).
).