По общепринятой терминологии непрерывную функцию называют функцией класса  (нулевой гладкости). В дальнейшем нам потребуются траектории и кривые более высокого порядка гладкости.

ОПРЕДЕЛЕНИЕ. Траектория называется непрерывно дифференцируемой, если функция непрерывно дифференцируема, то есть существует и непрерывна функция , (в точках и рассматриваются односторонние производные).

В этом случае траектория относится к классу .

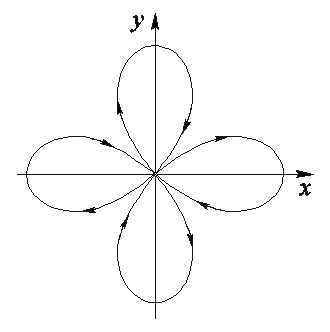
Пример. Траектория , имеющая вид четырехлистного цветка, непрерывно дифференцируема (рис. 9).

ОПРЕДЕЛЕНИЕ. Непрерывно дифференцируемая траектория называется гладкой, если , .

Замкнутая непрерывно дифференцируемая траектория называется гладкой, если , , и .

Пример. Траектория (окружность) – гладкая.

Требование гладкости равносильно требованию существования касательной к графику отображения и непрерывного вращения этой касательной при движении по графику.

ОПРЕДЕЛЕНИЕ. Траектория, составленная из конечного числа гладких траекторий, называется кусочно-гладкой.

Рисунок 9	Рисунок 10

Примеры. Траектория (дуга полукубической параболы, рис. 10,а – гладкая; траектории и – кусочно-гладкие (рис. 10,б). Отметим, что кусочно-гладкие траектории и отличаются друг от друга тем, что – непрерывно дифференцируемая траектория, а таковой не является.

Если – гладкая траектория, то эквивалентные ей траектории, как обычно, получаются заменой параметра по указанной выше формуле , , дающей непрерывную строго возрастающую функцию. Но такая замена без дополнительных условий может перевести гладкую траекторию в негладкую. Потребуем, чтобы замена параметра была непрерывно дифференцируемой функцией с положительной производной.

ОПРЕДЕЛЕНИЕ. Гладкой кривой называется класс траекторий, получающийся из гладкой траектории всевозможными непрерывно дифференцируемыми заменами с положительной производной.

Можно дать другое определение гладкой кривой: гладкой кривой называется класс траекторий, в котором есть гладкая траектория.

Определение кусочно-гладкой кривой предоставляется читателю.

Заметим, что в математике есть другие определения кривой (как, например, геометрического места точек, или множества точек, удовлетворяющих некоторому уравнению, и т.д.).