Тригонометрическая форма удобна для осуществления и геометрического представления операций умножения и деления комплексных чисел.

Согласно определению произведения комплексных чисел и имеем

.

Используя формулы косинуса и синуса суммы углов и алгебраическую запись комплексного числа, получаем  и окончательно .

Видим, что модуль произведения двух комплексных чисел равен произведению их модулей, а аргумент (с точностью до слагаемого, кратного ) – сумме аргументов сомножителей. Это свойство распространяется на конечное число сомножителей , и дается формулой

.

Следует иметь в виду, что даже если каждый угол , то вычисленный по данной формуле аргумент произведения может отличаться от на слагаемое, кратное .

Пример. Для произведения комплексных чисел  и имеем но .

Рисунок 2

На рис. 2 показано построение произведения : для треугольника с вершинами в точках построен подобный треугольник с вершинами . Углы этих треугольников равны в общей вершине и равны в вершинах .

По определению, частное, полученное от деления комплексного числа на комплексное число , , дается формулой  которая при принимает вид

Непосредственная проверка показывает, что . Это равенство позволяет представить операцию деления на операцией умножения на . Поэтому достаточно ограничиться построением точки и использовать известное геометрическое изображение произведения.

 

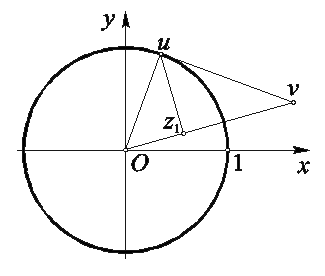
Рисунок 3

Будем считать сначала, что точка лежит в круге радиуса 1 и с центром в нуле (рис. 3). Из точки , , восстановим перпендикуляр к лучу, идущему из 0 через точку . В точке пересечения перпендикуляра с окружностью проведем касательную к окружности и отметим точку пересечения касательной с лучом. Из подобия прямоугольного треугольника с вершинами треугольнику с вершинами имеем равенство или .

О точке говорят, что она получена инверсией точки относительно рассматриваемой окружности или, иначе, точки симметричны относительно окружности радиуса 1. Аргументы точек и одинаковы и пусть равны . Имеем

.

Точка симметрична точке относительно действительной оси. Положим , то есть = . Построение окончено.

Видим, что точка получена из симметрией относительно окружности и симметрией относительно действительной оси.

Если , то построение точки следует вести в обратном порядке.

Точке , преобразование инверсии ставит в соответствие эту же точку и получается как точка, симметричная относительно действительной оси.

Возвращаясь к формуле , представив комплексные числа в тригонометрической форме , , имеем