В аналитической химии существует два типа задач на расчет химических равновесий с помощью ЗДМ:

1) расчет равновесных концентраций реагирующих частиц (атомов, ионов, молекул) по заданным значениям их исходных концентраций и константам равновесия химических превращений в системе (прямая задача моделирования равновесий);

2) расчет констант равновесия химических превращений и исходных концентраций реагирующих частиц по массиву экспериментальных данных, функционально связанных с равновесными концентрациями химических форм в растворе (обратная задача моделирования равновесий).

В учебный курс аналитической химии включены только прямые задачи по расчету химических равновесий.

Предположим, что в водном растворе находится двухпротонная кислота Н₂А. В таком растворе образуются следующие равновесные системы:

Запишем уравнение материального баланса для кислоты Н₂А

c_H₂A= [H₂A] + [HA⁻] + [A²⁻].

Наряду с этим можно записать еще уравнение электронейтральности раствора

Эти выражения составляют систему 4 уравнений для 4 неизвестных: [H⁺], [HA⁻] [A²⁻] и [H₂A], точное решение которой является нелегкой задачей. Однако во многих случаях прямую задачу по расчету химических равновесий можно решить с приемлемой точностью упрощенным способом, если расчеты проводить с использованием суммарной константы равновесия.

Предположим, что в растворе образуются соединения АВ и QR, которые частично диссоциируют по реакциям

АВ ↔ А⁺ + В⁻;

QR ↔ Q⁺ + R⁻,

а ионы А⁺ и R⁻ взаимодействуют с образованием AR_n^(n-1)− по реакции

A⁺+nR^- ↔ AR_n^(n-1)-.

Запишем суммарную реакцию:

Общая (суммарная) константа равновесия в этой системе 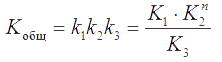используется для решения задачи определения равновесной концентрации соединения AR_n^(n-1)− по заданным исходным концентрациям соединений АВ и QR с помощью ЗДМ.

В подобных задачах почти всегда приходится решать уравнения высоких степеней. Однако их часто можно предельно упростить, если в качестве одной из неизвестных концентраций взять минимальную, чтобы иметь возможность пренебречь ею при расчете алгебраических сумм (пример 4). При этом если константа равновесия реакции велика, то в качестве неизвестной берут равновесную концентрацию одного из исходных компонентов реакции, а если она мала – то равновесную концентрацию продукта реакции.

Пример 4. Вычислить равновесные концентрации всех ионов после завершения реакции

6Fe²⁺ + Cr₂O₇²⁻ + 14H⁺ ↔ 6Fe³⁺ + 2Cr³⁺ + 7H₂O,

константа равновесия которой K = 10⁵⁶, если исходные молярные концентрации компонентов реакции с(Fe²⁺) = 0,3 M; c(Cr₂O₇²⁻) = 0,01 M; c(H⁺) = 0,07 M.

Решение. Константа велика, равновесие реакции сдвинуто вправо, поэтому минимальную концентрацию следует искать среди равновесных концентраций исходных веществ.

Воспользуемся следующим алгоритмом решения задачи; под компонентами равновесия реакции (R) выписываем в первой строке исходные концентрации участников реакции (с), в следующей строке – равновесные концентрации [R] и в последней строке – убыль исходных концентраций (у). (Размерность опускают, поскольку значения начальных и равновесных концентраций всегда выражены в моль/л раствора).

Из условий задачи видно, что минимальной будет концентрация ионов водорода, поскольку концентрации других ионов взяты в избытке. Удобно за первую неизвестную концентрацию (х) взять не саму величину [H⁺], а кратную ей 14х, т.е. положить [H⁺] = 14х.

Найдем выражения для остальных равновесных концентраций. Для этого сначала получим выражения для убыли (у) исходных концентраций всех компонентов реакции. Начнем с убыли концентрации ионов водорода. Если начальная концентрация этих ионов 0,07 М, а их равновесная концентрация 14х, то убыль y_H⁺ составляет 0,07 – 14х.

Для расчета убыли концентрации ионов Fe²⁺ воспользуемся правилом эквивалентности:

6Fe²⁺	—	14H⁺
y(_Fe²⁺)	—	(0,07 – 14x).

Решая эту пропорцию, находим: y(_Fe²⁺)= 3(0,01 – 2х) = 0,03 – 6х. Тогда равновесная концентрация [Fe²⁺] = 0,3 – 0,03 + 6x = 0,27 + 6x.

Аналогично этому

Cr₂O₇²⁻	—	14H⁺
y(_{Cr₂O₇²⁻})	—	(0,07 – 14x).

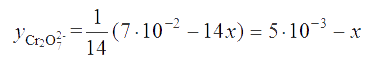
Следовательно, равновесная концентрация [Cr₂O₇²⁻] = 0,01 – 5×10^-3 + х = 5×10^-3 + х.

Выразим теперь равновесную концентрацию ионов Fe³⁺:

6Fe³⁺	—	14H⁺
[Fe³⁺]	—	(0,07 – 14x).

Отсюда имеем .

Осталось выразить равновесную концентрацию ионов Cr³⁺:

2Cr³⁺	—	14H⁺
[Cr³⁺]	—	(0,07 – 14x).

Следовательно, .

В итоге получаем следующую равновесную систему:

R	Fe²⁺	Cr₂O₇²^-	H⁺	Fe³⁺	Cr³⁺
с	0,3	0,01	0,07
[R]	0,27 + 6x	5×10^-³ + x	14x	0,03 - 6x	10^-² - 2x
y	0,03 - 6x	5×10^-³ - x	0,07 - 14x

Запишем для нее константу равновесия:

Подставим сюда найденные выражения для равновесных концентраций ионов:

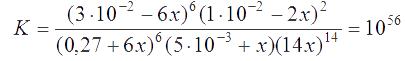
Это уравнение легко решить приближенно, поскольку вторыми слагаемыми в алгебраических суммах ввиду малости значений х можно пренебречь. В результате получаем решение: х = 2×10^-6. Таким образом, концентрации ионов при установившемся равновесии равны: [H⁺] = 14x = 2,8×10^-5 M; [Fe²⁺] = 0,27 + 6x ≅ 0,27 М; [Cr₂O₇²^-] = 5×10^-3 + x = 5,002×10^-3 M; [Fe³⁺] = 0,03 - 6x = 2,999×10^-2 M; [Cr³⁺] = 0,01 - 2x = 9,996×10^-3 M.

Если минимальная концентрация сопоставима по величине с другими равновесными концентрациями веществ в системе, то приходится решать уравнения высоких степеней по общим правилам, используя, например, итерационную процедуру Ньютона.