Чтобы найти условия получения максимальной буферной емкости, рассмотрим уравнение (2.19). Учитывая, что  dc_OH¯= dc_A¯ = dc_HA, имеем

.

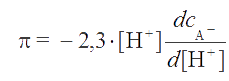(2.22)

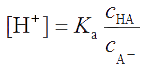
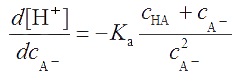Из выражения определяем

.

(2.23)

Подставляя (2.23) в (2.22), приходим к выражению .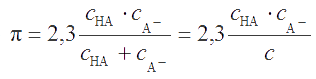

В точке максимума функции π = f(c_A¯) производная dπ/dc_A¯ = 0, что выполняется, если c_HA = c_A¯ =c / 2. Следовательно максимальная емкость буферного раствора имеет место при равной концентрации его компонентов. Для определенного соотношения c_HA/c_A¯ буферная емкость пропорциональна общей концентрации с.

Поскольку, согласно уравнению (2.20), величина π зависит также от рН, можно дифференцированием уравнения (2.21) и приравниванием к нулю производной dπ/d[H⁺] показать, что при условии

максимальная буферная емкость π_max достигается, когда

Произведя эту замену в уравнении (2.21), получаем выражение для расчета максимального значения буферной емкости раствора, состав которого удовлетворяет условиям (2.24) и (2.25):

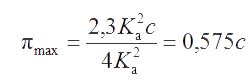(2.26)

Соотношение c_HA/c_A¯ обычно находится в пределах от 10:1 до 1:10, так что область буферного действия охватывает значения рН = рК_а ± 1. Рецептуры приготовления буферных растворов для разных интервалов рН можно найти в справочных руководствах или составить буферные смеси самим (пример 26).