Амфолиты - это соединения, в растворах которых сосуществуют как протонодонорные, так и протоноакцепторные частицы. К ним относятся так называемые «кислые соли» (NaHCO3, NaH2PO4), соли катионокислот и анионооснований, аминокислоты (например, глицин NH2CH2COOH) и другие соединения.
Растворы кислых солей. При добавлении амфолита (КtНA – cоль двухпротонной кислоты Н2А) к воде он может действовать как кислота или основание, а вода подвергаться самопроизвольной ионизации:
Согласно стехиометрии реакций уравнение материального баланса для ионов Н+ имеет вид [H+] = [A2-] + [OH¯] – [H2A]. Подставляя в него концентрации [A2-], [OH¯] и [H2A], найденные из уравнений для констант равновесий, получаем:
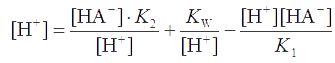
Преобразуем это уравнение, помножив на [H+]K1, откуда найдем [H+]:
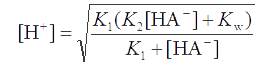
По формуле (2.6) можно наиболее точно рассчитать рН в растворах анионооснований, являющихся продуктами ступенчатой диссоциации анионов многопротонных кислот (пример 16). Это уравнение можно упростить, применяя приближенные значения. Если концентрация соли KtHA равна с, а K1 и K2 различаются так, что [H2A] и [A2−] << [HA-] (пример 17), то можно допустить, что [HA-] ≅ c. Константа Kw часто бывает пренебрежимо мала по сравнению с произведением К2с. При этих условиях имеем:
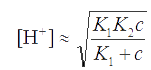
Если же с >> К1, то уравнение для [H+] приобретает еще более простой вид:
(2.8)
Таким образом, концентрация ионов H+ в первом приближении не зависит от концентрации соли (пример 18). Из уравнения (2.8) видно, что если К1К2 > Kw, то раствор имеет кислую реакцию, если, наоборот, К1К<Kw, то реакция среды щелочная.
В растворах солей катионокислот и анионооснований ВН+А (пример 19) устанавливаются равновесия
ВН+ + Н2О ↔ Н3О+ + В;
А- + Н2О ↔ НА + ОН¯.
Поскольку [H+] = [B] - [HA], то, пренебрегая автопротолизом воды и выражая [B] и [HA] из уравнений для констант кислотности катиона ВН+ и основности аниона А-
и принимая во внимание, что для сопряженных протолитов , получаем
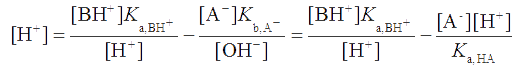
Или после несложных преобразований , откуда
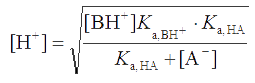
Так как Ka,HA << [A-], допустима аппроксимация
Если Ka,HA и Ka,BH+ близки, то [BH+] ≈ [A−]. Тогда приходим к формуле
(2.9)
идентичной формуле (2.8).
Пример 16. Рассчитать рН в 0,01 М растворе NaHS (Ka,H2S = 1,0×10-7; Ka,HS- = 1,3×10-13).
Решение. Так как cHS- >> Ka,H2S, но Ka,HS− · cHS- ≈ KW, то, используя формулу (2.6), находим .PNG)
Пример 17. Рассчитать рН в 0,01 М растворе глицина NH2CH2COOH.
Решение. В растворе глицина, который можно рассматривать как двухосновную кислоту NH3+CH2COOH с Ка,1 = КW / Kb= 3,2×10-3 и Ка,2 = 2,0×10-10, устанавливаются равновесия:
Как видно, Ка,1 близко к с, но Ка,2 ·с > KW. Поэтому, используя формулу (2.7), получаем .PNG)
Пример 18.
Рассчитать рН в 0,1 М растворе NH4CN (Ка,NH4+ = 5,7×10-10; Ка,HCN = 6,6×10-10).
Решение. Поскольку константы кислотности близки и Ка,NH4+ · cNH4+ >> KW, то, согласно формуле (2.9), 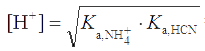
Пример 19. Рассчитать рН в 0,1 М растворе (NH4)2HPO4.
Решение. В растворе гидрофосфата аммония устанавливаются равновесия:
NH4+ + H2O ↔ NH3 + H3O+; Ка,NH4+ = 5,7×10-10,
HPO42− + H2O ↔ H2PO42− + OH−; KW/Ка,H2PO4- = 10-14/6,2×10-8 = 1,6×10-7,
HPO42− + H2O ↔ PO43− + H3O+; Ка,HPO42-= 4,7×10-13.
Так как Ка,NH4+ и Ка,H2PO4- >> Ка,HPO42-, то основной вклад в общую концентрацию ионов водорода вносят два первых равновесия. В этом растворе в роли кислоты выступает ион NH4+, а в роли основания – ион H2PO4-. Поэтому, используя формулу (2.9), находим:
.PNG)

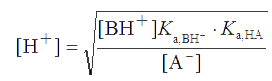
.PNG)