Теорема 2.2 (Bryant, 1986). Две булевы функции равны тогда и только тогда, когда их ROBDD изоморфны для заданного порядка переменных.

 

В заключение хотелось бы отметить ряд интересных свойств ROBDD. ROBDD позволяют компактно представлять булевы функции, кроме этого, существуют эффективные алгоритмы для выполнения всех типов логических операций на ROBDD. Все эти свойства основаны на ключевом факте, что для любой булевой функции существует точно одна ROBDD, представляющая ее. Это означает, что для функции константа 1 (или константа 0) существует точно одна ROBDD, состоящая из терминальной вершины 1 (0). И задача определения, является ли функция булевой константой, выполняется за константное время (вспомним, что эта задача для формул является NP-полной). Так ROBDD, состоящая из одной терминальной вершины 1, независимо от порядка переменных представляет функцию константа 1. Таким образом, для проверки тавтологии достаточно за константное время проверить, состоит ли ROBDD из одной терминальной вершины 1. Аналогично решается задача выполнимости по ROBDD. Для того чтобы определить равенство двух булевых функций воспользуемся теоремой 2.2. По условию теоремы достаточно, построить их ROBDD и проверить совпадение узлов.

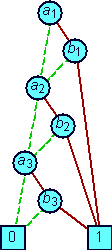
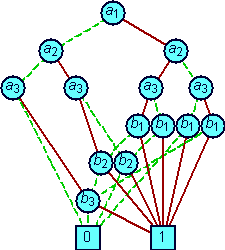
Выбор порядка переменных p при построении ROBDD существенно влияет на ее размер. Рассмотрим функцию f = (a₁ b₁) `vv` (a₂ b₂) `vv`  (a₃ b₃), построим для этой функции две диаграммы для порядка `pi_1` = {a₁ < b₁ < a₂ < b₂ < a₃ < b₃} и для порядка `pi_2`  = {a₁ < a₂ < a₃ < b₁ < b₂ < b₃}. В первом случае ROBDD состоит из 8 узлов (рис. 2.5, а), во втором случае ROBDD состоит из 16 узлов (рис. 2.5, б).

 

 

 

а) ____________ б)

Рис. 2.5. Две ROBDD для функции f = (a₁ b₁) `vv` (a₂ b₂) `vv` (a₃ b₃): а – для порядка `pi_1` = {a₁ < b₁ < a₂ < b₂ < a₃ < b₃}; б – для порядка `pi_2` = {a₁ < a₂ < a₃ < b₁ < b₂ < b₃}