Интенсивность светового пучка, очевидно, представлена первым элементом вектора-параметра Стокса I = S₀. Условие полной поляризации пучка излучения определяется выражением

S₀² = S₁² + S₂² + S₃²

Заметим, что и левая и правая части (19) инвариантны относительно преобразования координат. Для случая неполяризованного пучка S₁² = S₂² = S₃² = 0. Частично поляризованный пучок характеризуется неравенством

S₀² > S₁² + S₂² + S₃²

Поскольку для вектора – параметра Стокса справедливо свойство аддитивности, то любой частично поляризованный пучок можно представить в виде суммы векторов поляризованной и неполяризованной составляющих частей пучка

S = S^(e) + S^(p)
или
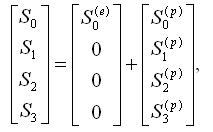(20)

где S₀^(e) - единственный отличный от 0 параметр Стокса неполяризованной части пучка; S_i^(p) - параметры Стокса полностью поляризованной части пучка, удовлетворяющие соотношению аналогичному (19).

Из уравнения (19) без труда находим

(21)

Отношение интенсивности поляризованной части пучка к полной интенсивности получило название степени поляризации

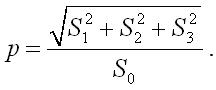(22)

Видно, что степень поляризации p может принимать значения от 0 до 1.

Если плоскость референции Q (например, плоскость (XOY) повернуть относительно оси OZ на угол φ против часовой стрелки, то значения параметров Стокса в новом базисе изменятся в соответствии с преобразованием

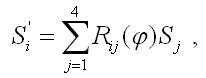(23)

где R_ij – элементы матрицы

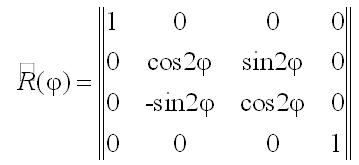(24)

которая носит название: оператор поворота плоскости референции.

Величины S₀, p, S₃ инвариантны относительно поворота плоскости референции, следовательно, их можно использовать для описания состояния поляризации независимо от выбора плоскости Q. Два других параметра S₁ и S₂ зависят от преимущественного направления φ₀ колебаний электрического вектора в пучке относительно выбранной плоскости Q и поэтому при повороте плоскости референции на угол φ определяется как

S'₁ = S₀ pcos2(φ₀ + φ)
S'₂ = S₀ pcos2(φ₀ + φ)(25)