Определение кодов Хемминга легко обобщить на случай q- ичных кодов для q>2. Достаточно просто заметить, что главная идея построения таких кодов состоит в определении матрицы H, любая пара столбцов которой линейно независима. Однако в случае q>2 для задания проверочной матрицы нельзя использовать все не нулевые q- ичные последовательности длины m над полем GF(q), поскольку некоторые пары линейно зависимы. Например, в поле {0,1,2} из трех элементов векторы 11 и 22 линейно зависимы, так как в этом поле сложение осуществляется по модулю 3 и следовательно 11 + 22 = 00. Чтобы обеспечить линейную независимость, выберем в качестве столбцов матрицы все последовательности длины m, у которых первая ненулевая компонента равна единице. Тогда все столбцы будут попарно линейно независимыми, а некоторые тройки столбцов могут оказаться линейно зависимыми, и минимальный вес в коде будет равен трем (теорема 1.3).

Всего существует  таких различных столбцов. Следовательно, можно построить код Хэмминга с длиной кодового слова  и числом информационных символов () - m. Код Хемминга, исправляющий одиночные ошибки, существует для каждого q, которое является степенью простого числа, и для любого m>1.

Например (13,10) - код Хемминга над GF(3) задается проверочной матрицей

и порождающей матрицей

Второй пример линейного не двоичного кода носит практический характер. Предположим, что ЭВМ и периферийное устройство связаны кабелем, по которому параллельно передаются 4 бита. Четыре бита представляют один 16-ричный символ, и передается последовательность таких информационных символов. Нам бы хотелось объединить символы в блоки и защитить каждый блок от одиночных ошибок. Взяв q = 16 и m = 2, мы видим, что можно было бы получить (17,15) - код Хемминга над полем Галуа GF(16) с 16 элементами. Используя это поле, можно построить порождающую матрицу (17,15) - кода Хемминга над полем GF(16) и с ее помощью выписать следующие соотношения для проверочных символов:

,

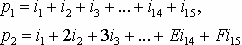где буквы A, B, C, D, E F, G используются соответственно для представления 16-ричных символов 10 (1010), 11 (1011), 12 (1100), 13 (1101), 14 (1110) и 15 (1111). После каждого блока из 15 информационных символов ставятся соответствующие два проверочных символа. Используя это, декодер может исправлять одиночные ошибки в блоке из 17 символов. Поле Галуа GF(16) существует и может быть построено как алгебра многочленов с коэффициентами из множества {0,1} по модулю неприводимого многочлена p(x) = x⁴ + x + 1.