При осреднении по Рейнольдсу все зависимые переменные исходных уравнений Навье–Стокса разбиваются на среднюю (осреднённую по ансамблю или по времени) и пульсационную компоненты. Для компонент скорости:

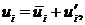
где и 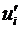– средняя и пульсационная компоненты скорости соответсвенно (i=1,2,3).

Аналогичным образом для давления и других скалярных величин:

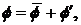
где 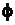обозначает скалярную величину такую, как, например, давление, энергия или концентрация примеси.

Подставляя выражения этой формы для переменных течения в первоначальные уравнения неразрывности и количества движения и проводя осреднение по времени (или по ансамблю) и опуская черту сверху для средних величин, получаем уравнения следующего вида:

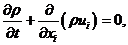(6.1)

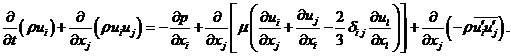(6.2)

Уравнения (6.1) и (6.2) называются уравнениями Рейнольдса. Они имеют такую же форму, как и первоначальные уравнения Навье–Стокса, однако скорости и другие переменные решения являются осреднёнными по времени (по ансамблю). Появляются дополнительные члены, которые представляют собой влияние турбулентности. Эти напряжения Рейнольдса 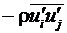необходимо моделировать для замыкания системы (6.1) – (6.2).