3.3. Граничные интегральные уравнения

Граничные интегральные уравнения можно получить различными способами, используя интегральные тождества (формулы Грина, теорему взаимности Бетти теории упругости), метод взвешенных невязок и т. п., которые на границе расчетной области связывают два решения. В качестве одного из решений используют фундаментальные решения.

Теорема взаимности Бетти представляется в виде:

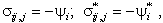
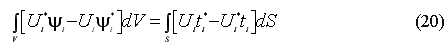
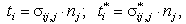
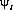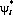где и - объемные силы. Эта теорема связывает два решения теории упругост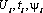и и .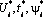

Используем в (20) фундаментальные решения (16) и (19) в качестве решений 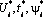. После подстановки в (20) фундаментальных решений с учетом 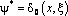и с учетом свойств дельта-функции Дирака, получим:

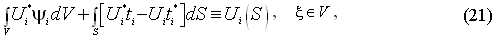
Последнее выражение представляет собой тождество Сомильяны.

Здесь точки x=ξ всегда выбираются внутри расчетной области, а не на границе. Тождество Сомильяны позволяет вычислять перемещения во внутренних точках области по известным решениям теории упругости на границе.

Граничные интегральные уравнения теории упругости можно получить, подставляя в формулу (21) выражения (16) и (19), если точки ξ – точки приложения сосредоточенных сил для фундаментальных решений - выбираются на поверхности тела.

Точки ξ называют «полюсами».

Рассматривается набор полюсов, число которых равно числу точек поверхности, в которых ищутся неизвестные значения перемещений или усилий. Назовем эти точки «узлами». Обычно «полюса», т. е. ξ выбираются непосредственно в узлах. В этом случае число граничных интегральных уравнений равно числу неизвестных значений перемещений или усилий в узловых точках поверхности. Полученные интегральные уравнения являются сингулярными (т. е →∞ в т. x= ξ ), поскольку сингулярны фундаментальные решения (16) и (19). Вопросы вычисления сингулярных интегралов исследованы С. Г. Михлиным. В решениях (16) сингулярность слабая. Интегралы от функций со слабой особенностью всегда существуют как несобственные даже при .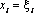

В решениях (19) сингулярность имеет порядок 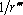, где m – размерность пространства .

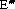Определим правило вычисления таких интегралов.

Рассмотрим гладкую поверхность в окрестности полюса ξ₀.

Вырежем точку ξ₀ полусферой радиуса ε с центром в точке ξ₀. Вычислим сингулярную часть интеграла от 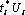по полусфере , когда ξ→ ξ₀ на границе S изнутри рассматриваемой области.

С.Г. Михлиным показано, что в граничных интегральных уравнениях интегралы с особенностями порядка 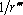существуют только при определенных условиях в смысле главного значения по Коши: при вычислении сингулярной части интеграла в пределе при ξ→ ξ₀ вырезанная область долж-на сжиматься симметрично относительно точки ξ₀. Введем локальную систему координат: ξ= ξ₀ в (19) и учитывая

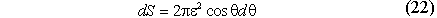
в результате получим при ε→0

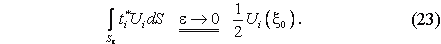
Следовательно:

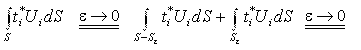
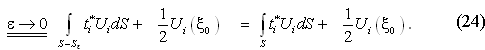
В уравнении (24) интеграл в правой части понимается в смысле главного значения по Коши несобственных интегралов, а «свободный член» всегда имеет знак плюс.

Если в точке ξ₀ на поверхности нельзя провести единственную касательную плоскость, т. е. точка ξ₀ является угловой, то коэффициент при свободном члене будет равным ω/4π, где ω- величина телесного угла в точке ξ₀, ω=2π для гладкой поверхности.

Подставив (24) в формулу Сомильяны (21), получим граничное интегральное уравнение теории упругости:

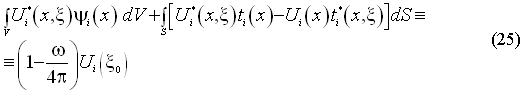
где 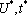задаются выражениями (16) и (19).

В граничном интегральном уравнении (25) часть граничных значений перемещений 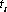 и усилий  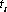заданы как граничные условия. Ставится задача вычисления оставшейся неизвестной части граничных перемещений или усилий. Это определяет первый этап численной реализации метода граничных интегральных уравнений теории упругости. На втором этапе численной реализации вычисляются значения перемещений, деформации и напряжения во внутренних точках расчетной области.

Как мы уже знаем, для вычисления перемещений 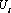во внутренних точках расчетной области по известным граничным значениям 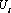и 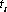 на границе используется формула Сомильяны (21). В выражениях (21), (25) интегрирование ведется по координате x, а свободный член определен в полюсе, т. е. является функцией от аргумента ξ. Поэтому для вычисления производных по координатам от перемещений 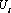по координатам дифференцирование производится по переменным ξ, а значит, дифференцирование можно вносить под знак интеграла.

   

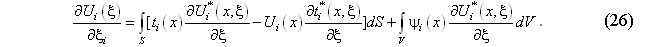
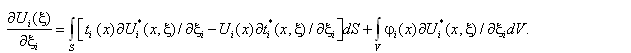
Уравнение (26) применяется для определения полей производных от перемещения по координатам во внутренних точках области после решения граничной задачи. Найденные таким образом производные oт перемещений используются для построения полей деформаций и напряжений в интересующих зонах деформируемого тела.

Возможность определять значения производных от перемещений по координатам, а значит определять деформации и напряжения в квадратурах (26), не прибегая к численному дифференцированию, является важным преимуществом МГЭ, поскольку этот способ более точный. Кроме того, поля деформаций и напряжений можно и имеет смысл определять лишь в важных для исследователя зонах (таких, как зоны концентрации напряжений или деформаций, определяющие работоспособность конструкции), что позволяет уменьшить время расчета, а также количество получаемой информации.