Обычно первичные данные существуют или с использованием тех или иных операций приводятся к одному из двух наиболее широко распространенных представлений поверхностей (полей) в ГИС: растровому представлению (модели) и модели TIN.

Растровые ЦМР представляют собой матрицу высот: регулярную (обычно квадратную) сеть высотных отметок в ее узлах, расстояние между которыми (шаг) определяет ее пространственное разрешение. Преимущество такой модели — в удобстве ее компьютерной обработки. В последнее время довольно часто для обозначения таких моделей используется термин GRID (грид). К растровой, или как ее чаще называют матричной или регулярной, модели путем интерполяции, аппроксимации, сглаживания и иных трансформаций могут быть приведены ЦМР всех иных типов, что чаще всего и делается на практике. Для восстановления поля высот в любой его точке (например, в узле регулярной сети) по заданному множеству высотных отметок (например, по цифровым записям горизонталей) обычно применяются разнообразные методы интерполяции. Среди них наиболее употребительными считаются метод кригинга, средневзвешенная интерполяция по методу Шепарда, полиномиальное и кусочно-полиномиальное сглаживание.

Суть модели TIN в ее наименовании — «Нерегулярная треугольная сеть» (в английском оригинале — Triangulated Irregular Network). В своем пространственном выражении — это сеть треугольников — элементов триангуляции Делоне — с высотными отметками в ее узлах, что позволяет представить моделируемую поверхность как многогранную. Триангуляцией Делоне для множества точек S  на плоскости называют триангуляцию DT(S), такую что никакая точка A из S не содержится внутри окружности, описанной вокруг треугольника из DT(S), такого, что ни одной из вершин его не является точка A. Такая триангуляция максимизирует минимальный угол среди всех углов всех построенных треугольников, тем самым избегаются «тонкие» треугольники.

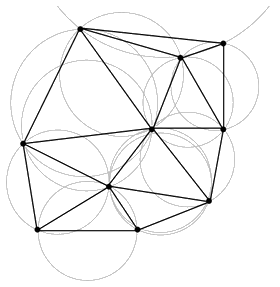
Рис.1.2 Триангуляция Делоне

Модель TIN поддерживается многими мощными универсальными программными средствами ГИС, модулями обработки и создания ЦМР в их составе. Таков, к примеру, модуль 3D Analyst в программных средствах ГИС Arclnfo (ESRI Inc., США). Однако ее использование в технологиях создания ЦМР на основе слоя оцифрованных горизонталей цифровых карт, массовое производство которых налажено большинством национальных топографо-картографических служб, вскрыло его существенные недостатки. Основной из них — «эффект террас», выражающийся в появлении морфологических артефактов — плоских участков в заведомо невозможной геоморфологической ситуации (например, по линии днища V-образных тальвегов). Одна из основных причин — в малости расстояний между точками цифровой записи горизонталей в сравнении с расстояниями между самими горизонталями, что характерно для большинства типов рельефа в их картографическом отображении. Появление таких морфологических артефактов нарушает морфографию и морфометрию моделируемого рельефа и снижает точность и качество самой модели и ее производных. Один из способов значительного улучшения качества и морфологического правдоподобия ЦМР состоит в расширении модели TIN путем ее структурирования — введения в нее сети тальвегов, водоразделов и линий разрывов (бровок, уступов террас и т.п.).

Обратной (двойственной) триангуляции Делоне являются полиномы Вороного. Эти фигуры образуются при соединении середин сторон треугольников, образовывающих триангуляционную сеть. Такие модели практически не используются для отображения рельефа. Большее применение полиномы Вороного нашли для моделирования погребенных поверхностей и создания каркасных моделей рудных тел в горно-геологических ГИС.

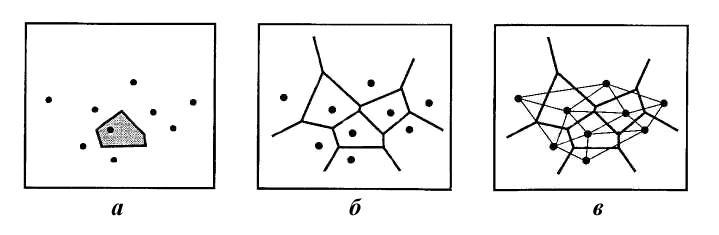
Рис. 1.3 Многоугольник Вороного (а), диаграмма Вороного (б), та же диаграмма Вороного и двойственная ей триангуляция Делоне (в)

Дальнейшее развитие цифрового моделирования рельефа связывается с новыми трехмерными моделями пространственных данных, известными пока лишь в экспериментах и немногих реализациях в коммерческих программных средствах ГИС. Эти модели основаны на трехмерных расширениях «планиметрических» двухмерных моделей. К ним принадлежат модель объемных пикселов — «вокселов» (трехмерное расширение растровой модели данных) и трехмерное расширение модели TIN — тетраэдрическая модель. Оба типа «истинно-трехмерных» моделей способны описывать не только поверхности, но и тела, заимствуя подходы и алгоритмы так называемого «твердотельного моделирования» в компьютерной графике. Известны примеры их использования в геологии, геофизике, маркшейдерии как инструмента «геометризации недр».