Понятие топологии. Топология бумажной карты. Спагетти-модель. Необъектная линейно-узловая топология. Объектная топология. Топология базы геоданных.

Понятие топологии.

Все способы организации векторных данных относятся к одному из двух основных типов векторных моделей данных: топологические векторные модели данных и нетопологические векторные модели данных.

Простые векторные модели, как правило, не используют топологию и хорошо подходят для систем компьютерной картографии. Более продвинутые векторные модели, как правило, основаны на топологии и предназначены для выполнения аналитических операций

Топология, устанавливает пространственные отношения между географическими объектами, является основополагающим свойством для гарантии качества данных. Топология делает возможным проведение расширенного пространственного анализа и играет фундаментальную роль в обеспечении качества базы данных ГИС.

Топологические отношения являются одним из наиболее полезных видов отношений, поддерживаемых пространственными базами данных. Топологическая структура данных определяет, где и как точки и линии соединяются в узлах на карте, порядок соединения, определяет форму дуги или полигона.

Чтобы разобраться с топологией в ГИС, нужно различать топологию пространства и топологию фигуры, которая находится в этом пространстве.

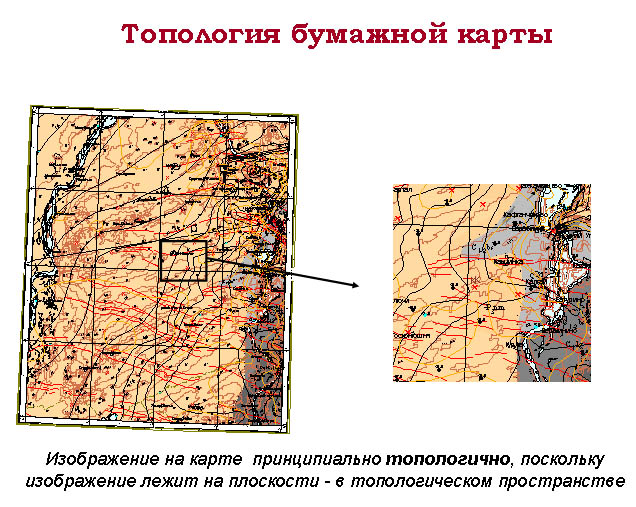
Картография занимается отображением (моделированием) метрических пространств, причём выполняется это на плоскости - также метрическом пространстве. В картографии принципиально работают с топологическими пространствами и обойти это нет не только необходимости, но и возможности. Другим словами, изображение на карте - принципиально топологично, поскольку изображение лежит на плоскости - в топологическом пространстве. Действительно, если нарисовать карту на плоской резине, а потом растянуть её в разных направлениях, то фигуры (картографические изображения) деформируются, но отношения (связи) между их элементами останутся без изменений; смежные линии разных фигур, как бы связанные своими концами с другими элементами, так и остались в этом "виде". Изменятся лишь формы линий.

Можно выделить следующие типы топологических отношений [В.Г.Горбачев, 1997г.]:

• Необъектные топологические отношения: Линейно-узловые топологические отношения;
• Объектные топологические отношения:
• Внутриобъектные топологические отношения
• Межобъектные топологические отношения:
• Узловые топологические отношения
• Межобъектные топологические отношения в пределах одного слоя
• Межслойные топологические отношения между объектами;
• Топологические межобъектные ресурсные связи;
• Концептуальные топологические отношения (отношения между классами объектов, или, логические связи).

В понятие топологии объекта заложено понятие топологии объектов, принятых в разделе математики, изучающей топологические свойства фигур.

В ГИС понятие топологии редуцировано. Здесь под топологией понимаются именно пространственные отношения между географическими объектами, а топология самих объектов принимается существующей по умолчанию во всех моделях векторных данных ГИС.  Наличие или отсутствие в моделях векторных данных топологических пространственные отношения между объектами позволяет говорить о топологических или нетопологических моделях векторных данных.

Внутриобъектные топологические отношения

Главным понятием здесь является ОБЪЕКТ. Объекты могут быть:

1. точками (символы);

2. линиями (отрезок) либо полилиния (связанная последовательность отрезков прямой). Здесь реализуется связность частей, на чём базируется внутриобъектная топология. Её сразу закладывают в понятие объекта и в его создаваемую структуру.

3. полигональными объектами (замкнутая полилиния). Реализуются операции создания и редактирования полигонального объекта таким образом, что последний всегда остаётся замкнутым.

Таким образом, в ГИС первичен объект, который по определению сам по себе является целостным и топологичным. Объект всегда целостный, поскольку каждый тип объекта создаётся своей специфической операцией.

Таким образом, в ГИС, объект - это автономная топологическая конструкция, над которой можно выполнить следующие операции:

а) создать объект;

б) уничтожить объект;

в) переместить объект в другое место;

г) скопировать объект в другое место.

Нетопологическая модель векторных данных: спагетти-модель.

Простейшей векторной структурой данных является спагетти-модель [Dangermond, 1982], которая, по сути, переводит "один в один" графическое изображение бумажной карты. Возможно, она представляется большинством из нас как наиболее естественная или наиболее логичная, в основном потому, что карта реализуется как умозрительная модель. Хотя название звучит несколько странно, оно на самом деле весьма точно, по сути. Если представить себе каждый графический объект нашей бумажной карты кусочком (одним или несколькими) макарон, то вы получите достаточно точное изображение того, как эта модель работает. Каждый кусочек действует как один примитив: очень короткие - для точек, более длинные - для отрезков прямых, наборы отрезков, соединенных концами, - для границ областей. Каждый примитив — одна логическая запись в компьютере, записанная как строки переменной длины пар координат (X,Y).

В этой модели соседние области должны иметь разные цепочки спагетти для общих сторон. То есть, не существует областей, для которых какая-либо цепочка спагетти была бы общей. Каждая сторона каждой области имеет свой уникальный набор линий и пар координат. Хотя, конечно, общие стороны областей, даже будучи записанными, отдельно в компьютере, должны иметь одинаковые наборы координат.

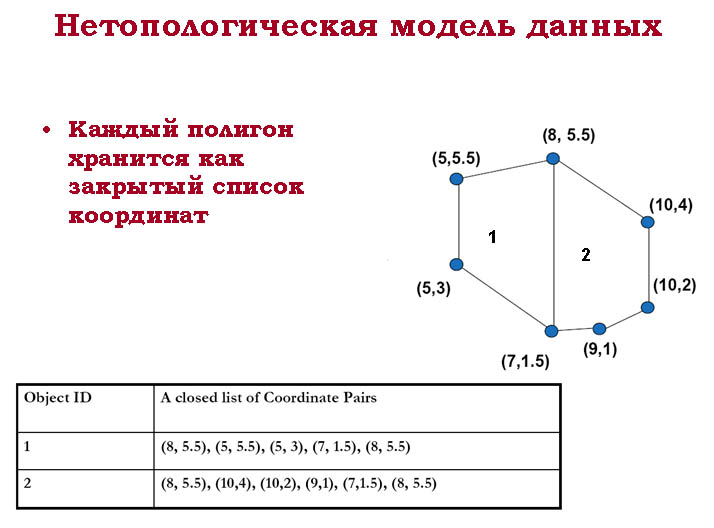
Поскольку спагетти-модель выглядит как перевод "один к одному" аналоговой карты, пространственные отношения между объектами (топология), например, такие, как положение смежных областей, - подразумеваются, а не записываются в компьютер в явном виде. И все отношения между всеми объектами должны вычисляться независимо. Результатом отсутствия такого явного описания отношений между объектами является огромная дополнительная вычислительная нагрузка, которая затрудняет измерения и анализ. Но так как спагетти-модель очень сильно напоминает бумажную карту, она является эффективным методом картографического отображения и все еще часто используется в компьютеризованной картографии, где анализ не является главной целью. Кроме того, это представление оказывается весьма близким к языку управления многих плоттеров, что упрощает процесс вывода карт на печать. Отрисовка на плоттере данных спагетти-модели обычно довольно быстрая  по сравнению с  отрисовкой  других моделей.

<

Топология: определение пространственных взаимосвязей.

В отличие от спагетти-модели, топологические модели [Dangermond, 1982], как это следует из названия, содержат топологическую информацию в явном виде.

Рассмотрим топологическую модель данных на примере модели данных покрытия ARC/INFO – одного из форматов данных, который многие годы считался одной из наиболее удачных разработок компании ERSI.

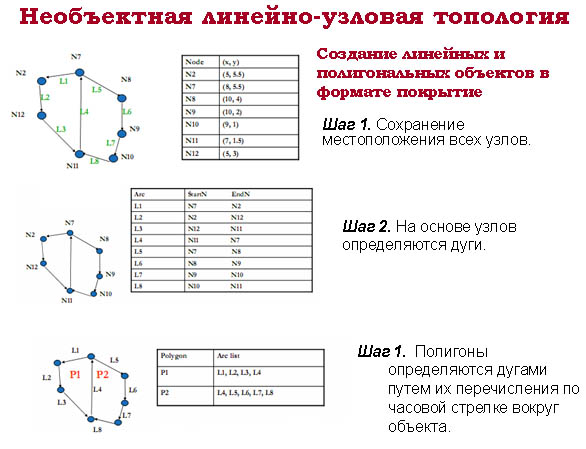
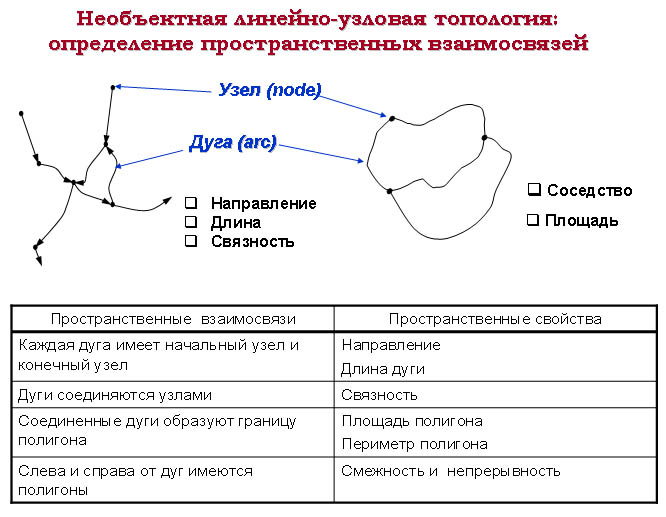
Топологическая информация описывается набором узлов и дуг. Узел (node) — больше, чем просто точка, обычно это пересечение двух или более дуг, и его номер используется для ссылки на любую дугу, которой он принадлежит. Каждая дуга (аrс) начинается и заканчивается либо в точке пересечения с другой дугой, либо в узле, не принадлежащем другим дугам.

Топология представляет математическую процедуру, которая определяет пространственные свойства и взаимосвязи, включающие: связность и длины дуг, направление дуг, смежность и площади полигонов.

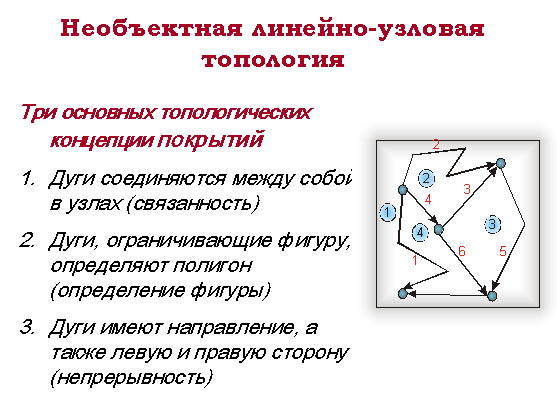
Пространственные взаимосвязи описываются  пространственными свойствами.

Линейно-узловая топология.

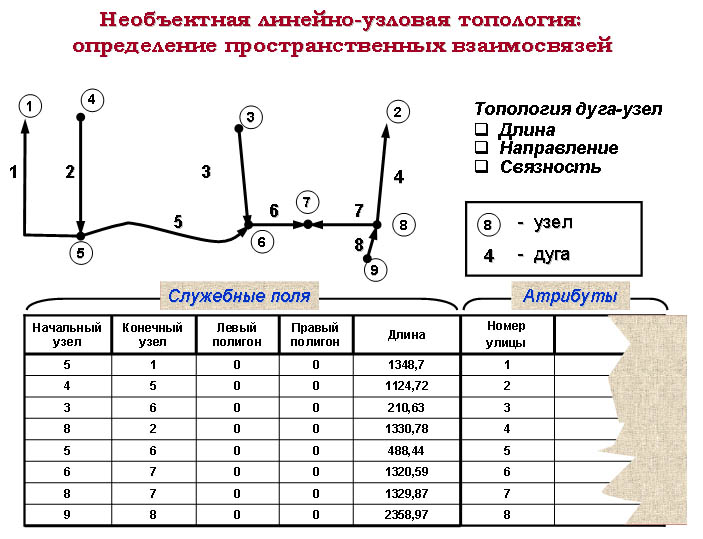
Линейно-узловая топология (дуга-узел) выражает пространственные взаимосвязи между дугами и узлами: она определяет длину, направление, связность. Географический анализ опирается на эти свойства. 

Узлы. From-node – начальная точка дуги, to-node – конечная точка дуги. Они определяют, как цифровались ваши данные. Направление дуг важно, если вы моделируете направленные потоки (например, реки или движение транспорта). Информация о топологии хранится в специальных таблицах.

Длина дуги измеряется от начального узла  (from-node) до конечного узла (to-node). Единицами измерения длины являются единицы измерения картографической проекции.

Направление дуги определяется от начального узла (from node) к конечному узлу (to-node).

Связность. Дуги соединяются узлом. По определению дуги с номерами 4,7,8 на слайде соединены, поскольку каждая из них имеет общий узел с номером 8. Таблица внизу показывает эти пространственные отношения.

Полигонально-линейная топология представляет пространственные взаимосвязи между дугами и полигонами, которые ограничиваются дугами; она определяет площадь и соседство. Географический анализ также опирается на эти свойства.

Определение площади. Когда дуги или наборы дуг соединяются, чтобы образовать замкнутую фигуру, границы определяют площадь полигона. Этот набор дуг хранится как список, определяющий полигоны, который они образовали. Список дуг, образующих полигон, хранится в отдельном файле.

Соседство. Два полигона соседние, если у них общая дуга. Программа (ARC/INFO)  нумерует полигоны и хранит их  как левый полигон (LPOLY#) и правый полигон (RPOLY#). Один и тот же полигон может быть левым полигоном в отношении одной дуги и правым полигоном по отношению к другой дуге.

Вы можете представить концепцию левого и правого полигона, вообразив, что вы путешествуете вдоль дуги, как будто по дороге. Ваша исходная точка - это начальный узел (from-node) и вы направляетесь к конечному узлу (to-node). Площадь слева от вас - левый полигон, площадь справа - правый полигон.

Обратите внимание, что полигон 5 и левый, и правый в верхнем списке. Полигон 5 является правым полигоном в отношении дуг под номером 6 и 10, но он же и левый полигон по отношению к дуге 14.

Внешний полигон. Когда ARC/INFO строит полигонально-линейную топологию, всегда создается один "внешний" полигон, представляющий площадь, которая остается за границами покрытия. Дуги, определяющие внешние границы вашего полигонального покрытия, являются внутренней границей внешнего полигона.

*   У внешнего полигона всегда  код (ID) = -1 .

*   Внешний полигон иногда определяют как фоновый полигон и его площадь равна суммарной площади полигонов покрытия.

База геоданных: геометрия пространственных объектов.

В 1999 году компания ESRI выпустила в свет свою последнюю разработку – новый формат географических данных, - который называется база геоданных.

Базы геоданных реализуют объектно-ориентированную модель данных ГИС. В базе геоданных каждый пространственный объект хранится в виде строки таблицы. Векторная форма объекта хранится в поле формы объекта, а атрибуты - в других полях. В каждой таблице хранится класс объектов.

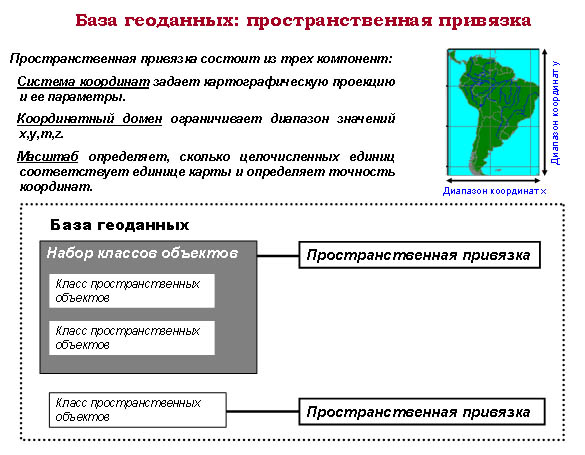
В дополнение к пространственным объектам базы геоданных могут хранить растры, таблицы данных и ссылки на другие таблицы. Базы геоданных - это хранилища, позволяющие держать все пространственные данные в одном месте. Их можно определить как СУБД с добавлением покрытий, шейп-файлов и растров. Однако, в них имеются также важные новые возможности, отсутствующие в файловой модели данных.

Одно из преимуществ базы геоданных в том, что в ней можно задавать поведение объектов; все пространственные объ­екты базы геоданных хранятся в одной базе данных, при этом большие классы объектов базы геоданных можно хранить, не разделяя на части.

Помимо общих объектов, таких как точки линии, полигоны, можно создавать пользовательские объекты, например, трансформаторы, трубопроводы или участки. Для пользовательских объектов можно определить специальное поведение, что позволяет лучше представить объекты реально­го мира. Поведение объектов можно использовать для под­держки сложного моделирования сетей, предотвращения ошибок при вводе данных, особого способа визуализации объектов, создания собственных форм для проверки или ввода атрибутов объектов.

Поскольку возможно создание собственных пользовательских классов объектов, количество классов объектов неограниченно. Класс пространственных объектов имеет специальное поле, хранящее форму и положение пространственных объектов. Это поле называется shape (форма), и оно является полем типа геометрия (geometry). Все пространственные объекты  в пределах одного класса пространственных объектов обладают одним типом геометрии. Базовыми геометрическими классами объектов (формами) являются точки, мультиточки, линии и полигоны. Вы можете также создавать объекты с новой геометрической формой.

База геоданных: отношения между объектами.

Объекты в реальном мире имеют отношения с другими объектами. Одни объекты имеют фиксированный пространственный экстент (на пример, леса), другие – не имеют (например, люди).

Одним из примеров  отношений между объектами является связь земельного участка с владельцем, зоной землепользования, учетной записью или зданием.

Желательно отслеживать эти отношения так, чтобы, когда один объект меняется, связанные с ним объекты могли реагировать. Например, когда удаляется инженерная опора, должны удаляться и все прикрепленные к ней трансформаторы и другое оборудование.

Формат базы геоданных имеет средства явного определения отношений среди пространственных и непространственных объектов.

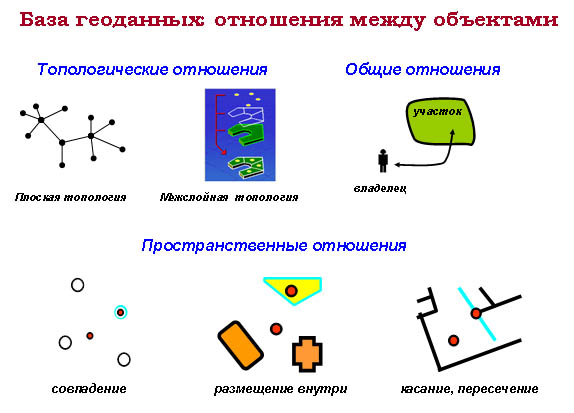
Различают три вида отношений: топологические, пространственные и общие.

Топологические отношения  встраиваются в данные в момент создания геометрической сети или плоской топологии (внутри одного класса). Топология базы геоданных аналогична топологии покрытия Arc/Info. Эти отношения позволяют быстро находить соседние полигоны или пересекающиеся линии. В базе геоданных кроме плоской топологии реализован еще один топологический механизм, позволяющий отслеживать пространственные отношения между объектами разных  классов пространственных объектов (между объектами разных слоев), осуществляя, таким образом, межслойную или трехмерную топологию. Например, если граница между государствами подходит по реке, то объекты линейного класса реки должны совпадать с объектами линейного класса граница. Или изолиния с нулевой отметкой должна точно соответствовать границе полигона, представляющего акваторию моря.

Пространственные связи.  ArcGIS ArcInfo  реализует богатый набор пространственных операций, которые позволяют определить такие пространственные отношения между объектами как касание, совпадение, пересечение, размещение внутри или вовне. Например, может быть решена такая задача: «Определить общую протяженность автомобильных дорог  Республики Татарстан» или «Найти все автомобильные дороги, пересекающие железнодорожную».

Логические отношения – формируют явную постоянную связь между пространственным или непространственным объектом из класса- источника с пространственным или непространственным объектом из класса- адресата.

Топология реализуется в виде набора правил целостности, определяющих поведение пространственно взаимосвязанных географических объектов и объектных классов. Топологические правила, применяемые к географическим объектам или объектным классам в базе геоданных, позволяют пользователям ГИС моделировать такие пространственные отношения как связность (связаны ли линии дорожной сети?) и смежность (существует ли промежуток между двумя полигонами участков?).

Топология полезна также для контроля целостности совпадающей геометрии у различных классов объектов (например, совпадает ли береговая линия и с границей страны?).

Топология создается и хранится как новый класс базы геоданных. Она хранит в себе:

1. Перечень участвующих в топологических отношениях классов (подтипов)

2. Кластерный допуск, ранги(топологические параметры) и правила

3. Имеющиеся топологические ошибки и исключения

4. Устанавливает и поддерживает требуемые пространственные взаимоотношения в момент проверки топологии

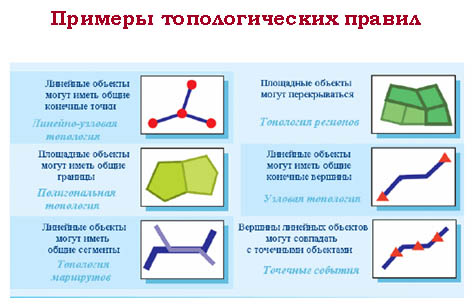
Топологические правила

Топологические правила могут быть заданы для объектов внутри объектного класса или для объектов, принадлежащих двум или более объектным классам. Примерами правил могут служить следующие условия: полигоны не могут перекрываться, линии не должны иметь висячих узлов, точки должны лежать в пределах границ полигона, между полигонами не должно быть промежутков, линии не должны пересекаться, точки должны быть расположены на конечных точках линий.

Правила используются для задания пространственных отношений между объектами внутри объектного класса, а также между объектами разных классов.

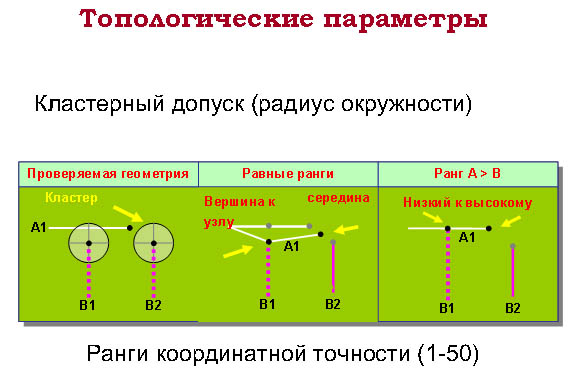
Топологические параметры

Кластерный допуск похож на допуск неразличимости. Это расстояние, на котором вершины считаются совпадающими. Вершины и конечные точки, попадающие в пределы кластерного допуска, замыкаются в процессе проверки топологии.

Ранги координатной точности задаются на уровне класса объектов и определяют, сколько объектов класса могут потенциально быть передвинуты по отношению к объектам других классов при проверке топологии. Чем выше ранг (единица является максимальным значением), тем меньше объектов будет передвинуто в процессе проверки топологии.

Домены и отношения

Атрибутивные домены – это правила, которые описывают допустимые (т.е. правильные с точки зрения вашей задачи) значения поля таблицы (атрибута). Один хранящийся в базе данных атрибутивный домен может использоваться несколькими классами пространственных объектов и таблицами. Однако совсем не обязательно, чтобы все объекты одного класса пространственных объектов или таблицы использовали один и тот же атрибутивный домен.

Отношения – это правила логического взаимодействия объектов различных классов между собой. При описании отношений выбирается два класса, один из которых является исходным (владельцем), а второй – целевым (подчиненным). Кардинальность (тип отношений) определяет возможное количество объектов в классе-адресате, которые могут быть связаны с одним объектом в классе-источнике. Чаще всего отношения определяются кардинальностью один ко многим (одному объекту исходного класса соответствует несколько объектов целевого класса).

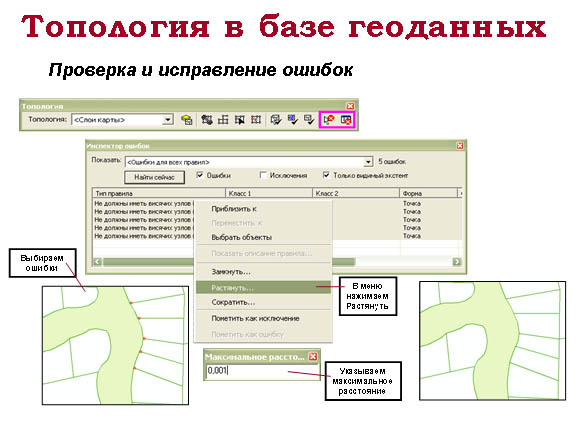
Проверка ошибок топологии

Операция проверки топологии используется для замыкания (слияния) геометрии объектов при попадании вершин в пределы кластерного допуска и для контроля нарушений заданных топологических правил. Проверка топологии начинается с замыкания вершин объектов на расстоянии меньше кластерного допуска, принимая в расчет ранг классов объектов (как это описано выше). Если вершины объектов находятся в пределах допуска, объекты из класса с минимальным рангом координатной точности будут передвинуты к объектам с более высоким рангом. В рамках процедуры замыкания во время операции проверки топологии также будут добавляться вершины в местах пересечения объектов, если такие вершины не существуют.

Также любые нарушения правил, обнаруженные в процессе проверки топологии, помечаются как ошибки.

Коррекция ошибок топологии

При обнаружении ошибок в процессе проверки топологии пользователь может действовать тремя путями:

1. Исправить ошибку при помощи инструмента Исправление топологической ошибки или другого метода.

2. Оставить ошибку без исправления.

3. Пометить ошибку как исключение. Инструмент Исправление топологической ошибки предлагает много способов коррекции в зависимости от типа ошибки и типа объекта.

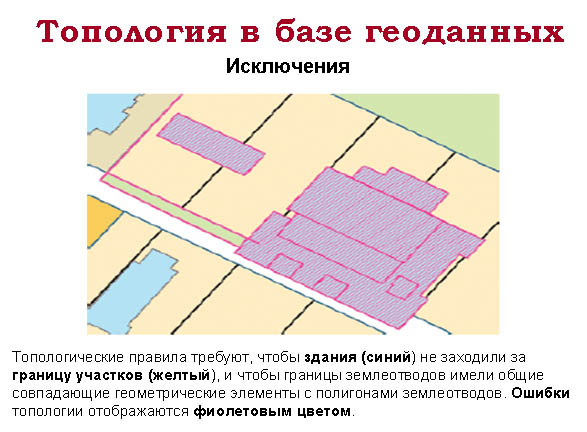
Исключения

При разрешении ситуаций с ошибками пользователь всегда может пометить отдельную ошибку или группу ошибок как исключение. Иногда появление определенной ошибки может быть допустимым. В таких случаях ошибка должна отмечаться как исключение. К примеру, если здание, показанное в нашем примере, является торговым центром, то такое здание, перекрывающее несколько земельных участков, не будет ошибкой, а исключением из правила. Когда ошибка помечена как исключение, она остается в этом качестве до тех пор, пока она не будет переустановлена вновь как ошибка. Запуск проверки топологии по той же области не покажет ошибку для варианта, помеченного как исключение.