Пространственные элементы. Описание пространственных элементов. Способы представления географического пространства. Модели данных: векторная, растровая. В лекции использованы материалы И.Ю. Черновой (КГУ)ю
Пространственные элементы. Представляемые на карте элементы, как природного происхождения, так и являющиеся результатом человеческой деятельности, называются объектами карты, или просто объектами.

Пространственные объекты окружающего мира легко можно разделить на 4 типа. Они представляют большинство природных и социальных элементов, которые мы встречаем каждый день. В ГИС объекты реального мира в основном представляются первыми тремя указанными типами объектов. Точки, линии и области представляются соответствующими символами, поверхности представляются путем добавление третьего измерения к исходным данным (высоты) либо специальными компьютерными средствами.
Точечные объекты – это объекты, которые в заданном масштабе не имеют длины и ширины и местоположение определяется только парой координат. В качество точечных объектов можно представить отдельно стоящие деревья, дома, населенные пункты, перекрестки дорог и т.д. О таких объектах говорят, что они дискретные, каждый их них в определенный момент времени может занимать только одну точку пространства.
Линейные объекты - это объекты, которые в заданном масштабе карты имеют длину, но не имеют ширины. Они представляются как бы одномерными в нашем пространстве. Такими объектами могут быть дороги, реки, границы, любые другие объекты, которые имеют большую протяженность, но небольшую ширину. Именно масштаб определяет порог, при пересечении которого мы считаем их объектами, не имеющими ширины.
Для линейных объектов, в отличии от точечных, мы можем указать пространственный размер простым определением их длины.
Площадные объекты (полигоны) – это объекты, которые при заданном масштабе имеют и длину и ширину («двумерные объекты»). Примерами полигонов может быть территория государства, города, озера и т.д. Границей полигональных объектов является линия, которая начинается и заканчивается в одной точке. Полигональные объекты имеют несколько характеристик: местоположение линии, определяющей полигон, форма и ориентация линии, величины периметра и площади полигона.
Добавление третьего измерения к полигональным объектам позволяет наблюдать и фиксировать поверхности (холмы, долины, скалы и тд). Поверхности могут описываться с указанием местоположения, занимаемой площади, ориентации и с добавлением третьего измерения, высот. Поверхности состоят из бесконечного числа точек со значениями высот. Мы считаем, что они непрерывны, поскольку эти точки распределены без разрывов, непрерывно, по всей поверхности. Использование таких вычислений весьма полезна, когда необходимо узнать, каков объем воды в водоеме, объем выбранного материала в карьере и т.д. Таким образом, поверхности являются 3-х мерными пространственными объектами.
Значения атрибутов. Шкалы измерений.
Геометрические примитивы – точки, линии, полигоны, помогают показать на карте объекты реального мира. Используя их, мы можем показать местоположение объекта и его форму. Но для того, чтобы совокупность геометрических объектов получила информативность карты, каждый из них должен обладать определенным набором описательных характеристик, интересных для пользователя, или атрибутов.
Использование атрибутов объектов определяется возможностью их измерения и сравнения с другими подобными объектами.
Существует устоявшаяся основа для измерения практически всех видов данных, в том числе и географических. Это шкалы измерения данных, которые простираются от простого наименования объектов до высокоточных измерений, позволяющих непосредственно сравнивать качества различных объектов. Использование определенной шкалы будет определяться отчасти тем, что мы классифицируем, отчасти тем, что мы хотим знать, отчасти нашими возможностями производить измерения при заданном масштабе наблюдения.
В таблице представлена связь шкал измерений с тремя типами географических объектов.

Номинальная шкала позволяет показать различные категории схожих объектов. Все объекты с одинаковым значением в чем-то похожи и отличаются от других объектов. Например: категории дороги: автострады, шоссе, второстепенные местные дороги. В номинальной шкале мы можем сказать, что объекты разных категорий различны, но как они отличаются – нет. Эта система не позволяет делать прямого сравнения объектов, за исключением определения тождества. Значение категорий можно представить, используя числовые коды или текст.
Для проведения более тонкое сравнение объектов используют порядковую (ранговую) шкалу. Порядковые (ранговые) шкалы позволяют расположить объекты по порядку, от большего к меньшему на качественном уровне (больше – меньше, светлее – темнее, лучше- хуже). Ранги представляют собой качественную или относительную величину и используются в случае, когда нет возможности провести точные измерения (например, территории, ранжированные для проведения отдыха – замечательный, хороший, средний, плохой). Поскольку оценка по рангам относительна, то при сравнении ориентируются только на установленный порядок, не зная абсолютного различия между рангами. Типичным примером является шкала Мооса для измерения твердости минералов. Можно назначать ранги, основываясь на атрибуте, (только тип или категория), а также на комбинации атрибутов. Например, классифицировать почвы по набору атрибутов –тип увлажнения + определенная пригодность для сельского хозяйства по набору признаков.
Другим ограничением порядковых (ранговых) шкал является то, что используя их мы не можем сравнить объекты количественно: по Шкале Мооса твердость гипса – 2, корунда - 9, алмаза- 10. Абсолютная же микротвердость этих минералов имеет следующие значения: гипса – 2,6 Па, корунда- 2 060Па, алмаза- 10 060 Па. Используя порядковую шкалу Мооса мы может только сказать, что алмаза тверже корунда и гипса, но утверждать, что алмаз тверже гипса в 5 раз, а корунд мягче алмаза всего на 1 было бы совсем неверно.

Самые точные измерения можно получить для атрибутов, измеренных в интервальной шкале, или шкале отношений, в которых измеряемым величинам приписывают численные значения. Атрибуты, измеренные в данных шкалах позволяют количественно сравнить объекты между собой. В данных шкалах можно измерить численность, количество и относительные значения параметров.

Численность и количество - показывают общие оценки. Численность представляет реальное число объектов на карте. Количество может быть любой измеренной величиной, связанной с объектом, например, число студентов в ВУЗе. Использование численности и количества позволяет узнать реальное значение каждого объекта, а также его реальную характеристику в сравнении с другими объектами.
Относительные значения – показывают взаимосвязь между двумя количественными величинами, и получаются делением одной величины на другую для каждого объекта. Использование относительных значений сглаживает разницу между большими и малыми регионами, или регионами с большим и малым числом объектов, при этом на карте будет более точно отображаться распределение объектов.
В качестве примера можно привести изучение температуры почвенного покрова в зависимости от содержания органического вещества в почвах. При сравнении карты-схемы Температура почв с картой распространения почв, мы знаем, что почвы светлые, бедные органическим веществом имеют температуру ниже, в интервале 8-15 0С (средняя температура - 140С). Почвы темные, богатые органическим веществом имеют температуру в интервале 20-240С (средняя температура – 23 0С). Теперь, имея среднюю температуру разных видов почв мы можем градуировать разницу между видами почв.
Существует некоторое ограничение при выполнении сравнений в интервальной шкале. При сравнении средней температуры почв мы получаем разницу в 9 0С. Но сказать, светлая почва в полтора раза холоднее темной мы не можем, так как начало шкалы Цельсия не является абсолютным нулем и связано с термодинамическими свойствами воды. Для такого сравнения необходимо перевести все величины в шкалу, где ноль представляет действительное начало температур, в шкалу Кельвина (К= 273 + 0С). Полученные результаты, 287 К и 296 К, не позволяют сказать, что температуры почв отличаются в полтора раза.
В результате перехода от шкалы Цельсия к шкале Кельвина мы перевели изучаемые величины в наиболее «количественную» шкалу измерений - шкалу отношений.
Данные в номинальной и порядковой (ранговой) шкалах являются дискретными значениями (одно и то же значение могут иметь несколько объектов). Данные в шкале интервалов/отношений (численность, количество и относительные величины)относятся к разряду непрерывных данных.
Способы представления географического пространства.
Многие реальные географические объекты имею форму с четким контуром. Говорят, что такие объекты дискретны. У дискретного объекта есть известная определенная граница. Можно точно определить, где объект начинается, и где он заканчивается. Озеро - это дискретный объект на карте ландшафта. Можно точно определить границу воды и суши. Другие примеры дискретных объектов: дороги, здания, участки. Дискретные объекты обычно бывают искусственными (созданными человеком) и обычно описываются векторным типом данных.

Непрерывные данные описывают объекты или явления, которые существуют в каждой точке пространства. Одним из типов непрерывных данных могут быть значения высот над уровнем моря. Примеры поверхностей такого типа - это распределение концентрации соли в почве или воде, уровня загрязнения от выброса загрязняющего вещества или ядерного реактора, огня от лесного пожара. На поверхности, отражающей концентрацию явления на рисунке справа, концентрация в любой точке будет функцией от способности явления двигаться через среду. Непрерывные данные обычно описываются растровым типом данных.
Существует другой тип непрерывных данных, которые относятся к непрерывным достаточно условно, и могут, в принципе, рассматриваться как дискретные данные. Примером таких данных могут быть данные, отражающие расселение популяций животных или плотность населения людей, распределение потенциальных клиентов магазина и распространение эпидемии, т.к. людям и другим живым организмам свойственно собираться в группы или стаи (т.е. образовывать дискретные объекты), а не расселяться по поверхности Земли равномерно.
Таким образом, многие объекты не являются явно непрерывными или явно дискретными. Создается единая среда представления географических объектов, в которой крайние случаи будут чисто дискретными или чисто непрерывными. Большинство явлений находится где-то между крайностями. Примерами объектов промежуточного типа могут быть типы почв, границы лесов, болот или географические границы рынков сбыта, на которые влияет телевизионная рекламная кампания. Из этого следует, что для представления дискретных данных может быть использована модель непрерывных данных – растровая модель, а для непрерывных данных– векторная модель.
Фактором определения положения объектов в диапазоне от непрерывных до дискретных явлений может быть простота выявления его границ. Если границу между шоссе и окружающими его полями можно определить довольно просто, то граница между болотом и заболоченным лугом определяется не столь очевидно и сетка растра, состоящая из ячеек, позволит представить ее с большей или меньшей точностью, не хуже, чем в векторном способе.
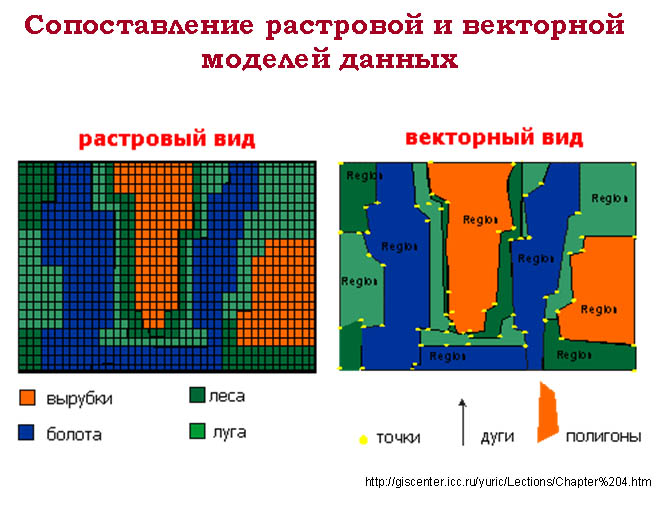
Растровый и векторный - два принципиально разных, но совершенно равноправных способа представления географического пространства, одинаково важны при изучении географического пространства. Выбор модели данных зависит от того, какие объекты мы собираемся исследовать, и какие методы исследования хотим применить.
Векторные модели.
Векторный метод представления данных позволяет создавать точные пространственные координаты явным образом. Это достигается приписыванием точкам пары координат (ХУ) координатного пространства, линиям – связной последовательности пар координат их вершин, полигонам – замкнутой последовательности соединенных линий, начальная и конечная точка которых совпадают.

Векторные объекты представляются в географическом пространстве точками, линиями, полигонами, либо в виде аннотаций. Существуют и более сложные виды геометрии векторных объектов – 3D Мульти-патчи, предназначенные для представления 3х мерных объектов.
Векторная модель данных основана на векторах (направленных отрезках прямых). Базовым примитивом является точка. Векторные линейные объекты создаются путем соединения точек прямыми линиями или дугами. Для описания дуги необходимо хотя бы 2 точки- начальную и конечную, для описания местоположения линейного объекта в пространстве. Если линия является кривой или ломанной, то необходимы дополнительные точки – точки перегиба (вертексы). Чем сложнее линия, тем больше точек требуется для ее описания.

Площадные объекты определяются набором линий. Для набора линий необходимо указывать из форму и ориентацию, а также величину площади, которую занимает описываемая площадь.

Векторная модель показывает геометрию картографических объектов. Чтобы придать свойства объектам, последние связывают с атрибутивными данными, хранящиеся в отдельном файле или в базе данных. В этом случае графические примитивы связываются с атрибутами посредством идентификаторов. Идентификаторы в большинстве случаев недоступны для пользователей и являются одним из ключевых элементов в различных форматах пространственных данных.

Типы векторных моделей данных.Существует несколько способов объединения векторных структур данных в векторную модель данных. Все способы относятся к одному из двух основных типов векторных моделей данных: топологические векторные модели данных и нетопологические векторные модели данных. Топология – это такой математический аппарат, который описывает пространственные отношения между объектами.
Простые векторные модели, как правило, не используют топологию и хорошо подходят для систем компьютерной картографии. Более продвинутые векторные модели, как правило, основаны на топологии и предназначены для выполнения аналитических операций.
Растровые модели.
Растровый метод использует принципиально другой способ представления географического пространства - разбиение пространства на множество элементов, каждый из которых представляет собой малую, но вполне определенную часть земной поверхности. Такой метод создает растровое изображение. Чаще всего использую квадраты, или ячейки, которые в растровых моделях одинаковы по размеру. Векторная модель представляет объекты дискретными, границы которых в пространстве четко определены, то растровый способ представляет географическое пространство в виде непрерывной поверхности, равномерно поделенной на равные ячейки.

Растры могут содержать информацию трех видов: тематические данные (тип растительности, ориентация или уклон склона и тд); данные дистанционного зондирования (аэрофо- и космосъемка); обычные цветные изображения (сканированные карты или фотографии). Растры используются для представления непрерывной информации: высоты местности, уклонов склонов, растительного покрова, зон распространения загрязняющих веществ и т.д.

Растровое изображение - это обычная двумерная матрица, в ячейках которой находится информация о цвете. Для каждой ячейки существует уникальный адрес, состоящий из номера строки и номера столбца.
Устройство пикселя. Характеризовать ячейку растра (или пиксела «picture element») можно двумя параметрами.

1. размер ячейки
2. количество цветов на ячейку - одна из важных характеристик изображения, которая сказывается на размере растра.
Пиксел имеет как значение, так и пространственное расположение.
В растровых системах есть два способа добавления атрибутивной информации об объектах. Простейшим является присвоение значения атрибута каждой ячейке растра (например, индекс растительности). Но в таком варианте каждая ячейка имеет только одно значение атрибута. Второй подход – связывание каждой ячейки растра с базой данных, так что любое число атрибутов может быть присвоено каждой ячейке растра.

Ячейки растра примыкают друг к другу для покрытия всей области. Поэтому мы можем использовать номера ячеек по вертикали и по горизонтали в качестве координат. Для определения местоположения прямоугольного растра в географическом пространства необходимо знать пару координат x, y хотя бы одного угла. В то же время, ячейки или пикселы результатов дистанционного зондирования сразу создаются в некоторой проекции, и для измерения на растр может быть помещена более точная координатная сетка.

Представление пространственных элементов в растровой и векторной моделях данных. Точечные объекты всегда будут представлены целым пикселем, линейные объекты будут представлены цепочкой смежных ячеек, полигоны – областью смежных ячеек.

Главный недостаток представления картографических данных в форме ячеек растра - это потеря точности информации о местоположении объектов. Вместо точных координат точек мы имеем отдельные ячейки растра, в которых эти точки находятся. Здесь мы наблюдаем изменение пространственной мерности, которая состоит в том, что мы изображаем объект, не имеющий измерений (точку), с помощью объекта (ячейки), имеющего и длину, и ширину. Чем меньше ячейка, тем меньше ее площадь, тем точнее она представляет точечный объект.
Легко увидеть, что эта структура данных изображает линии и полигоны ступенчатым образом. Точность представления данных зависит от масштаба и размера ячейки. Чем больше разрешение ячеек, и чем больше ячеек представляют определенную площадь, тем точнее это представление.
Значение ячейки.
Каждой ячейке растра присваивается определенное значение, служащее для идентификации или описания класса, категории, группы, к которым относится ячейка, либо для задания количественной характеристики свойства, которое описывает данный растр. Значение может представлять такие характеристики, как тип или структура почв, класс землепользования, стратиграфические подразделения. Значение может также представлять величину, расстояние или отношение в непрерывной поверхности данных. Высота, величина и направление уклона, уровень шума от аэропорта, величина pH почвы - примеры количественных характеристик.

В растрах, представляющих изображения, значения могут указывать цвет или спектральную отражающую способность. В этом случае каждой ячейке приписывается не одно, а несколько значений (мультиканальный растр).
Значения ячеек могут быть как целые, так и с плавающей запятой. Целочисленные значения удобны для представления значений дискретных данных, а значения с плавающей запятой - для представления непрерывных поверхностей.

Зоны. Любые две или более ячейки с одинаковым значением принадлежат к одной зоне. Зона может состоять из соединенных ячеек, несоединенных ячеек, или из тех и других. Зоны, ячейки которых соединены, представляют отдельные объекты территории, например, здание, озеро, дорогу или линию электропередачи. Каждая ячейка растра принадлежит к определенной зоне. Одни растры состоят из нескольких зон, другие - из множества зон.
Регионы. Каждая группа соединенных ячеек в зоне называется регионом. Зона, состоящая из одной группы соединенных ячеек, включает один регион. Зона может состоять из стольких регионов, сколько нужно для представления объекта; количество ячеек в одном регионе практически не ограничено. В растровом наборе данных на рисунке внизу, Зона 2 состоит из двух регионов, Зона 4 - из трех регионов, а Зона 5 - только из одного региона.
Значение ”Нет данных”. Если ячейке присвоено значение “Нет данных” (No Data), это означает, что данных о заданной характеристике в точке, которую представляет ячейка, либо нет, либо недостаточно. Значение отсутствия данных, иначе называемое пустым значением, обрабатывается всеми операторами и функциями иначе, чем другие значения. В большинстве случаев это значение передается в выходной растр, в других - ее значение формируется на основании значений соседних ячеек.
Для некоторых видов данных, чаще всего непрерывных, значение ячейки представляет измерение в центре ячейки. Пример – растр высот. Для изображения непрерывной поверхности, значения высот на границах ячеек вычисляют путем интерполяции, на основании известных значений ячеек, отнесенных к центральной точке.
В других случаях значение ячейки относится ко всей ее площади - поверхность отображается в виде «ступенек».
Пространственное разрешение растровых изображений. Растровые изображения в ГИС не имеют понятия масштаба. Изображения характеризуются таким понятием, как геометрическое разрешение растра. Оно характеризует площадь поверхности, изображенное в каждом пикселе. Если длина одной стороны пиксела соответствует 100м на местности, то говорят, что растр имеет геометрическое разрешение 100 м. При длине стороны пиксела, соответствующей 2 м на местности, говорят о растре с 2 метровым разрешением.

Разрешение возрастает при уменьшении размера ячейки, однако обычно за счет увеличения занятого дискового пространства и снижения скорости обработки. Уменьшение ячеек определенной области в два раза требует увеличения дисковой памяти примерно в четыре раза, в зависимости от типа данных и используемой технологии их хранения. Для большинства пользователей эффективность анализа более чем компенсирует потерю разрешения.
Сравнение представления пространственных элементов в растровой и векторной моделях данных. Растровые структуры не обеспечивают точной информации о местоположении, поскольку пространство поделено на дискретные ячейки конечного размера. Вместо точных координат точек мы имеем отдельные ячейки растра, в которых эти точки находятся. В этом случае точка, объект не имеющий измерений, изображается с помощью квадратной ячейки, имеющей длину и ширину; линии – как цепочки ячеек. Эта структура данных изображает линии ступенчатым образом. Таким же образом отображаются полигоны.
Местоположение точки на растре указать точнее, чем положений ячейки - нельзя. Чем больше размер ячейки, тем большую площадь земли она покрывает, тем меньше точность положений пространственных объектов.
Снижение пространственной точности положения объектов – главный недостаток растровой структуры данных. Увеличить точность можно увеличивая разрешение растра. При отображении одной и той же географической области с использованием растровой и векторной модели данных