1. Написать MPI-программу вычисления
интеграла 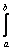 fx)dxс
точностью
fx)dxс
точностью 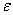 ,
используя обобщенную квадратурную формулу трапеций. Для оценки точности использовать
правило Рунге. Обеспечить равномерную загрузку всех процессорных элементов,
участвующих в работе программы. Вычислить ускорение и эффективность программы.
,
используя обобщенную квадратурную формулу трапеций. Для оценки точности использовать
правило Рунге. Обеспечить равномерную загрузку всех процессорных элементов,
участвующих в работе программы. Вычислить ускорение и эффективность программы.
2. Написать MPI-программу вычисления
интеграла 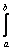 f(x)dxс точностью
f(x)dxс точностью 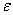 ,
используя обобщенную квадратурную формулу Симпсона. Для оценки точности использовать
правило Рунге. Обеспечить равномерную загрузку всех процессорных элементов,
участвующих в работе программы. Вычислить ускорение и эффективность программы.
,
используя обобщенную квадратурную формулу Симпсона. Для оценки точности использовать
правило Рунге. Обеспечить равномерную загрузку всех процессорных элементов,
участвующих в работе программы. Вычислить ускорение и эффективность программы.
3. Написать MPI-программу вычисления
интеграла 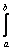 f(x)dxс
точностью
f(x)dxс
точностью 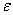 ,
используя обобщенную квадратурную формулу Ньютона («3/8»). Для оценки точности
использовать правило Рунге. Обеспечить равномерную загрузку всех процессорных
элементов, участвующих в работе программы. Вычислить ускорение и эффективность
программы.
,
используя обобщенную квадратурную формулу Ньютона («3/8»). Для оценки точности
использовать правило Рунге. Обеспечить равномерную загрузку всех процессорных
элементов, участвующих в работе программы. Вычислить ускорение и эффективность
программы.
Варианты заданий(1–3):
1. f(x)=exp(-x2+0.38)/(2+sin(1/(1.5+x2))), a=0.4, b=1.
2. f(x)=(x2+sin(0.48(x+2)))/(exp(x2)+0.38), a=0.4, b=0.6.
3. f(x)=(1-exp(0.7/x)/(2+x), a=1, b=3.
4. f(x)=exp(-tg(0.84x))/(0.35+cos(x)),
a=0, b=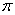 /2.
/2.
5. f(x)=arctg(0.7x)/(x+1.48), a=0.2, b=0.5.
6. f(x)=ln(1+x)/x, a=0.1, b=1.
7. f(x)=exp(-1.46x2)/(3.5+sin(x)), a=0.3, b=0.8.
8. f(x)=1/(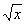 (exp(0.9x)+3)), a=0.5, b=2.
(exp(0.9x)+3)), a=0.5, b=2.
10. f(x)=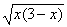 /(x+1), a=1, b=1.2.
/(x+1), a=1, b=1.2.
11. f(x)=exp(1-x)/(2+sin(1+x2)), a=0.4, b=1.
12. f(x)=sin(x+2)/(0.4+cos(x)), a=-1, b=1.
13. f(x)=(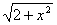 )/((1+cos2x)
)/((1+cos2x)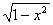 ), a=0, b=1.
), a=0, b=1.
14. f(x)=(x2+sin(0.48(x+2)))/(exp(x2)+o,38), a=0.4, b=1.
15. f(x)=arcsin(x/0.2)/x, a=1, b=1.6.
16. f(x)=x2 arcctg(x/2)/x, a=1, b=2.
17. f(x)=x/cos3(1.4x), a=0.1, b=1.
18. f(x)=x4 /(0.5x2+x+6), a=0.4, b=1.5.
19. f(x)=1/(x(0.2x+1)3/2, a=1, b=2.
20. f(x)=x/sin3(2x), a=0.1, b=0.5.
4. Написать MPI-программу вычисления
двукратного интеграла 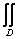 f(x,y)dxdy
методом Монте-Карло. Обеспечить равномерную загрузку всех процессорных элементов,
участвующих в работе программы; вычислить ускорение и эффективность программы.
f(x,y)dxdy
методом Монте-Карло. Обеспечить равномерную загрузку всех процессорных элементов,
участвующих в работе программы; вычислить ускорение и эффективность программы.
5. Написать MPI-программу вычисления
двукратного интеграла 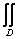 f(x,y)dxdy
методом повторного применения квадратурной формулы прямоугольников. Обеспечить
равномерную загрузку всех процессорных элементов, участвующих в работе программы;
вычислить ускорение и эффективность программы.
f(x,y)dxdy
методом повторного применения квадратурной формулы прямоугольников. Обеспечить
равномерную загрузку всех процессорных элементов, участвующих в работе программы;
вычислить ускорение и эффективность программы.
6. Написать MPI-программу вычисления
двукратного интеграла 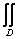 f(x,y)dxdy
методом повторного применения квадратурной формулы Симпсона. Обеспечить равномерную
загрузку всех процессорных элементов, участвующих в работе программы; вычислить
ускорение и эффективность программы.
f(x,y)dxdy
методом повторного применения квадратурной формулы Симпсона. Обеспечить равномерную
загрузку всех процессорных элементов, участвующих в работе программы; вычислить
ускорение и эффективность программы.
7. Написать MPI-программу вычисления
двукратного интеграла 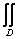 f(x,y)dxdy
методом повторного применения квадратурной формулы Ньютона («3/8»). Обеспечить
равномерную загрузку всех процессорных элементов, участвующих в работе программы;
вычислить ускорение и эффективность программы.
f(x,y)dxdy
методом повторного применения квадратурной формулы Ньютона («3/8»). Обеспечить
равномерную загрузку всех процессорных элементов, участвующих в работе программы;
вычислить ускорение и эффективность программы.
Варианты заданий (4-7):
1. f(x,y)=x/y2, D={0<x<1,2<y<5}.
2. f(x,y)=exp(x–y), D={-1 x
x 0,0
0,0 y
y 1 }.
1 }.
3. f(x,y)=xy, D={ x+2y
x+2y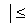 3,
3,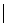 x–y
x–y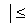 3}.
3}.
4. f(x,y)=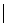 xy(x+y)
xy(x+y)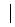 ,D={
,D={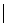 x
x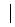 +
+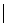 y
y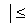 1}.
1}.
5. f(x,y)=(x2–y2)2,D={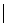 x
x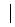 <y<1}.
<y<1}.
6. f(x,y)=exp(x+y)2,D={0<x<1,0<y<1–x}.
7. f(x,y)=(x2–y2)sin(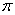 (x–y)2), D={
(x–y)2), D={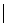 y
y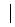 <x<1–
<x<1–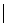 y
y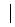 }.
}.
8. f(x,y)=(x4–y4), D={1<xy<2,1<x2–y2<2,x>0}.
9. f(x,y)=y2 (x2+1), D={1<xy<2,0<x<y<3x}.
10. f(x,y)=(xy)–2, где область D ограничена прямыми: y=3x, 3y=x, 5x+y=4, x+y=4.
11. f(x,y)=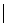 xy
xy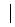 , D={x4+y4<1}.
, D={x4+y4<1}.
12. f(x,y)=x+y, где область D ограничена
прямыми: y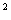 =2x, x+y=4, x+y=12.
=2x, x+y=4, x+y=12.
13. f(x,y)=(x+y)2/x, ), D={1<x+y<3,x<2y<4x}.
14. f(x,y)=x3+y 3,), D={x2<y<3x2,1<2xy<3}.
15. f(x,y)=cos(x2+y2), D={x2+y2<a2}.
16. f(x,y)=ln(1+x2+y2), D={x2+y2<a2,y>0}
17. f(x,y)=(xy)2, D={1<xy<2,
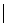 x–y
x–y
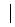 <1}.
<1}.
18. f(x,y)=exp(2x–x2), D={0<y<1,0<x<1–y}.
19. f(x,y)=xy+y2, D={0<x<2,0<y<2}.
20. f(x,y)=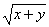 , D={0<x<1,0<y<x}.
, D={0<x<1,0<y<x}.