Сигнал, выработанный одним логическим элементом можно подавать на вход другого логического элемента. Это дает возможность образовывать цепочки из отдельных логических элементов. На рисунке 15 показаны примеры таких цепочек.

а)

б)

На рисунке 15 а) элемент ИЛИ (дизъюнктор) соединен с элементом НЕ (инвертор), а на рисунке 15 б) - элемент И (конъюнктор) с элементом НЕ (инвертор). Каждую такую цепочку будем называть логическим устройством: поскольку она состоит из нескольких элементов.

Цепочку из логических элементов будем называть логическим устройством. Схемы, соответствующие таким устройствам, называют функциональными .

На рисунке 16 приведен пример более сложной функциональной схемы.

Составить логическую схему по функциональной формуле достаточно просто. Например, функциональная схема, изображенная на рисунке 16, имеет два входа A и B. До поступления на конъюнктор B отрицается, а затем отрицается результат логического умножения. Все это приводит нас к формуле

,

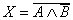(21)

которая представляет собой структурную формулу логического устройства. Важно научиться решать и обратную задачу: по структурной формуле вычерчивать соответствующую ей функциональную схему. Усложним задачу. Пусть имеется произвольная логическая функция, требуется построить функциональную схему.

Алгоритм решения такой задачи начинается с построения таблицы истинности. Затем в таблице следует определить одну или несколько строк, с результатом равным 1. На следующем шаге необходимо выписать комбинацию входных переменных, соединенных логическим умножением. Если входная переменная в нужной нам строке имеет значение 0, то она должна войти в логическое выражение с отрицанием. Полученные таким образом конъюнкции требуется логически сложить. Далее полученную формулу нужно сократить с использованием логических законов. Рассмотрим этот алгоритм на следующем примере.

Задача 7. Начертить функциональную схему, соответствующую таблице истинности.

Решение.

Рассмотрим строки, которые в столбце F(A,B) дают истину (эти строки в таблице выделены). Составим по первой строке выражение 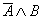(A следует отрицать, потому что в таблице стоит 0), аналогичное выражение по третьей строке дает 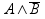. Соединяем два последних выражения союзом ИЛИ, получим 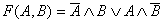. Вычерчиваем по логическому выражению функциональную схему.

Рисунок 17. Функциональная схема логической функции .

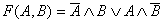Логическую функцию F(A,B)=Ā Λ B V A Λ 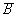называют операцией XOR (исключающее или) и обозначают .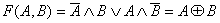

Еще один пример построения функциональной схемы.

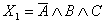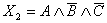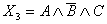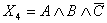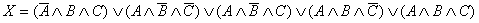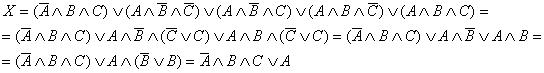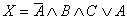Задача 8. Начертить функциональную схему, соответствующую таблице истинности. A B C результат 0 0 0 0 0 0 1 0 0 1 0 0 0 1 1 1 1 0 0 1 1 0 1 1 1 1 0 1 1 1 1 1 Решение. Выделяем в таблице строки, когда результатом функции является истина. A B C результат 0 1 1 1 1 0 0 1 1 0 1 1 1 1 0 1 1 1 1 1 Для первой строки последней таблицы имеем. , (22) для второй строки - , (23) для третьей строки - , (24) (24) для четвертой строки - , (25) (25) и для пятой строки - . (26) Соединяем выражения (22)-(26) логическим сложением. Будем иметь . (27) Теперь требуется упростить (27) на основе логических законов. . Таким образом, получили: . (28) Построим функциональную схему. Для этого потребуется отрицание A с последующим умножением на B, затем на C и, наконец, сложение с A. Полученная функциональная схема представлена на рисунке 18. Рисунок 18. Функциональная схема логической функции