Доказать законы алгебры высказываний можно:

Леонард Эйлер при решении задач изображал множества с помощью кругов, и в его честь этот метод был назван "методом кругов Эйлера". Однако такой прием очень полезен и при решении логических задач, когда с помощью кругов изображаются высказывания. Стоит отметить, что этим методом математики пользовались и до Эйлера. Так, в трудах Лейбница были обнаружены изображения таких кругов. Но, как уже говорилось, достаточно основательно этот метод был развит Эйлером. После Эйлера метод получил развитие в работах других ученых, однако наибольшего расцвета графические методы достигли в сочинениях английского логика Джона Венна, подробно изложившего их в книге "Символическая логика". Поэтому такие схемы называют "диаграммами Эйлера-Венна".

Любое высказывание на диаграмме изображается кругом, а его отрицание - частью плоскости, находящейся вне круга.

Если у нас есть два высказывания X и Y, то их на диаграмме изображают двумя кругами, как правило, разного цвета.

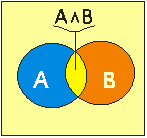
Ярким желтым цветом на диаграмме закрашено логическое умножение (конъюнкция) двух высказываний, а их логическое сложение (дизъюнкция) изображено на следующем рисунке. Другими словами логическое умножение - это пересечение кругов, а логическое сложение изображается как объединение кругов.

Давайте посмотрим, как с помощью диаграмм Эйлера-Венна можно доказать, что

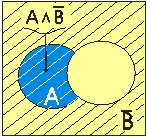
В соответствии с приоритетом логических операций, сначала требуется выполнить A Λ B (1 шаг), затем (2 шаг), (3 шаг) и, наконец, выполнить сложение высказываний, полученных на шагах 1 и 3 (4 шаг).

Шаг 1	Шаг 2	Шаг 3	Шаг 4

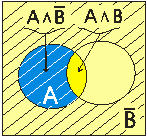На рисунке 8 (2 шаг) заштриховано высказывание , результат изображен голубым цветом с белой штриховкой (3 шаг). Из последнего рисунка (4 шаг) непосредственно видно, что .

С доказательством некоторых логических законов на диаграммах Эйлера-Венна и с помощью таблиц истинности можно ознакомиться по ссылке .