В рассмотренных выше системах счисления "вес" единицы любого разряда, кроме первого, всегда равнялся"весу" единицы предшествующего разряда, умноженному на постоянное основание системы Р. Можно, однако, привести пример такой системы счисления, в которой смысл понятия "основание системы счисления" заметно отличается от традиционного. Предлагаемая система является следствием расширения нашего представления о роли основания системы счисления. Сущность нового подхода легко представить, если рассмотреть счеты необычной конструкции.

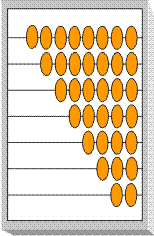
На нижней проволоке счет, отведенной для единиц младшего разряда, вес каждой из которых равен единице, помещено две косточки. На следующей проволоке помещено три косточки, на третьей - четыре и т.д., на n-ой проволоке - n+1 косточка.

Поскольку каждая косточка на второй проволоке заменяет две косточки, расположенные на первой проволоке, то вес этой косточки равен 2. Каждая косточка третьей проволоки заменяет три косточки второй проволоки, и, следовательно, ее вес в 6 = 3·2·1 раз больше веса косточки на первой проволоке. Из этих разъяснений следует, что косточка, расположенная на n-ой проволоке, имеет вес n!. Вес единиц от разряда к разряду растет, но неравномерно. Это приводит к представлению числа в следующем виде:

Получаем, что N-разрядное число, "списанное со счет", оказывается представленным не в виде суммы степеней основания Р, а в виде суммы факториалов n первых натуральных чисел.

Эту систему счисления относят к нетрадиционным позиционным и называют факториальной системой счисления.

Алгоритм перевода из десятичной системы счисления в факториальную очень прост. Он аналогичен алгоритму перевода из десятичной системы в Р-ичную путем деления на основание системы Р. Отличие в том, что в первый раз исходное десятичное число делим на 2, первое частное - на 3, второе частное - на 4 и т.д.

С числами этой системы можно выполнять арифметические действия по правилам, незначительно отличающимся от правил десятичной арифметики.

Как и в других системах счисления, в факториальной системе можно рассматривать дробные числа.

Каких-либо существенных практических применений этой системы, основанных на необычной сущности цифрового и многочленного представления, по-видимому, нет. Рассмотрение этой системы прежде всего полезно как методический подход в расширении представлений о системах счисления и обобщении принципа позиционности.

К нетрадиционным системам счисления относят и фибоначчиеву систему счисления.

Базисом фибоначчиевой системы является последовательность 1, 2, 3, 5, 8, 13, 21, 34, 55, ..., т.е. идущие подряд числа Фибоначчи.

Алфавитом этой системы счисления являются цифры 0 и 1. В записи числа в фибоначчиевой системе не могут стоять две единицы подряд.

Заметим, что системы, аналогичные фибоначчиевой, применяются при кодировании чисел. Это практически и теоретически интересные системы записи чисел. Изучение особенностей таких систем продолжается и в настоящее время.