Рассмотрим некоторое тело, находящееся в тепловом равновесии с излучением. Это значит следующее. Представим себе сначала несколько тел, нагретых до различной температуры, и для определенности поместим эти тела в полость, окруженную оболочкой с идеально отражающими стенками (рис. 5).

Рис. 5.	Рис. 6.

Даже если внутри этой полости будет абсолютный вакуум, тела будут обмениваться между собой энергией посредством электромагнитного излучения. При этом в результате такого теплообмена более нагретые тела будут охлаждаться, так как они испускают больше энергии, чем получают от окружающих тел, а менее нагретые тела – нагреваться, потому что они получают больше, чем отдают. Поскольку электромагнитные волны, излучаемые телами, распространяются с конечной скоростью, то пространство между телами будет заполнено энергией излучения. Опыт показывает, что в конце концов всегда устанавливается стационарное состояние (рис. 6), при котором все тела приобретают одинаковую температуру, т.е. поглощают в единицу времени ровно столько энергии, сколько и отдают, а плотность излучения в пространстве между телами достигает некоторой определенной величины, зависящей от температуры. Такое стационарное состояние и называется в данном случае равновесным.

Пусть – энергия, излученная 1 см поверхности данного тела в малом интервале длин волн , а – доля энергии падающего излучения, которое поглощается телом в этом интервале. Кирхгоф сумел доказать, что отношение зависит только от длины волны и температуры , и на его значение не влияют никакие другие характеристики тела (например, внутренняя структура или форма тела):

(1)

Таким образом, в формуле (1) – некоторая универсальная функция, зависящая только от длины волны и температуры. Интересно, что Кирхгоф получил уравнение (1), доказав, что его невыполнение приводит к возможности существования вечного двигателя. Новизна его теоремы заключалась не только в самом содержании, но и в достоверности и общности доказательства, основанного на молодой еще тогда термодинамике.

Далее, из условия равновесности и чисто геометрических соображений, легко показать (не будем на этом останавливаться), что функция очень просто связана с плотностью равновесного электромагнитного излучения , приходящегося на единичный интервал длин волн, которое установится в полости. А именно, и оказываются пропорциональными друг другу:

Задача, которую сформулировал и не смог решить Кирхгоф, состояла в экспериментальном и теоретическом определении универсальной функции , или, что фактически то же самое, функции .

Экспериментальное определение этих функций при заданной температуре во всем диапазоне длин волн было очень трудной задачей, на решение которой понадобилось 40 лет. Схематически графики этих знаменитых кривых представлены на рис. 7.

Рис. 7. Зависимость спектральной плотности равновесного излучения от длины волны.

Параллельно экспериментальным исследованиям предпринимались попытки теоретического определения функции . После постановки задачи Кирхгофом понадобилось примерно четверть века, чтобы осознать, что наблюдаемое явление равновесия между излучением и веществом принципиально противоречит всей классической физике.

Это можно пояснить простым примером. Предположим, что в нашу полость помещен кусок железа и его поверхность зачернена так, что он поглощает практически все падающее на него излучение (рис. 4). Известно с полной определенностью, что такой кусок при температуре 0 °С будет излучать с каждого квадратного сантиметра поверхности энергию в секунду, а при тепловом равновесии — одновременно и поглощать из окружающего пространства ровно такое же количество энергии в секунду. Используя пропорциональность и , тогда легко вычислить, что в той части пространства внутри полости, которая не занята частицами вещества, равновесная плотность энергии при 0 °С будет равна всего лишь . В то же время плотность тепловой энергии внутри самого куска железа при той же температуре равна приблизительно , т.е. в раз больше плотности энергии излучения (рис. 8). Эта тепловая энергия заключается в колебаниях атомов железа около положения равновесия. Таким образом, приходим к поразительному выводу: при термодинамическом равновесии между колеблющимися атомами вещества и электромагнитным излучением почти вся энергия сосредоточена в колеблющихся атомах, и лишь ничтожная ее часть приходится на долю излучения, находящегося с ними в равновесии.

Рис. 8. Железное тело в полости с абсолютно отражающими стенками в состоянии теплового равновесия.

Именно этот факт является совершенно непонятным с точки зрения классической физики. Это становится очевидным, если прибегнуть к следующей известной аналогии. Представим себе простую механическую модель рассмотренного нами опыта: на поверхности воды, налитой в какой-нибудь резервуар, плавают пробки, соединенные пружинами, так что пробки могут колебаться около положения равновесия. Если привести эти пробки в колебания, то они будут отдавать свою энергию воде, на поверхности которой появятся волны. Вследствие вязкости эти волны будут затухать, так что их энергия будет постепенно превращаться в тепло. Очевидно, что окончательный результат опыта будет состоять в том, что пробки прекратят колебания, а вся их энергия будет передана окружающей среде.

Невозможно представить, чтобы в конечном состоянии пробки находились в интенсивном колебании, а среда не получила бы никакой энергии. Но именно это имеет место в случае равновесия между нагретым материальным телом и излучением, когда почти вся энергия сосредоточена в колебаниях атомов, роль которых в механической аналогии играют пробки, а на излучение, т.е. «окружающую среду», приходится лишь ничтожная доля энергии.

Можно указать и конкретный закон классической физики, который здесь нарушается – это теорема о равномерном распределении энергии по степеням свободы. Вспомним, что согласно этой теореме на каждую степень свободы любой физической системы, находящейся в равновесии при температуре , приходится средняя кинетическая энергия, равная , где – постоянная Больцмана. В рамках классической физики эта теорема применима абсолютно к любой физической системе в равновесном состоянии, в том числе и к системе, которая состоит из куска железа и электромагнитного излучения. В данном случае число степеней свободы вещества равно , где – число атомов железа. Естественно, для макроскопического тела число огромно, но конечно. С другой стороны, электромагнитное поле с точки зрения классической физики представляет собой систему с бесконечным числом степеней свободы. Грубо говоря, это связано с тем, что для описания электромагнитного поля в каждый момент времени необходимо задать вектор напряженности электрического поля и вектор магнитной индукции в каждой точке полости . Поскольку число точек бесконечно, то бесконечно и число степеней свободы поля, т.е. число величин и , которые необходимо задать для однозначного определения конфигурации поля в данный момент времени. То же самое можно объяснить и немного иначе. Электромагнитное поле в полости можно представить как суперпозицию плоских монохроматических волн, каждая из которых характеризуется определенной амплитудой, направлением распространения и длиной волны. При этом в полости могут в принципе возбуждаться электромагнитные волны, в том числе и со сколь угодно малой длиной волны. При таком подсчете число независимых величин, характеризующих электромагнитное поле, также, очевидно, бесконечно. А это и есть число степеней свободы поля.

Таким образом, с точки зрения классической физики в задаче Кирхгофа мы имеем дело с равновесной системой, состоящей из двух подсистем: поглощающего и излучающего тела, число степеней свободы которого конечно, и находящегося с ним в равновесии электромагнитного поля, число степеней свободы которого бесконечно. Ясно, что для такой системы теорема о равнораспределении энергии по степеням свободы может быть выполнена только в том случае, если подавляющая часть энергии будет сосредоточена в электромагнитном поле, т.е. будет существовать в виде излучения. Таким образом, с точки зрения классической физики, равновесное состояние куска железа с окружающим его излучением наступит, когда атомы железа отдадут полю практически всю энергию. Это подтверждается точным теоретическим расчетом: в рамках классической физики для функции получается:

(2)

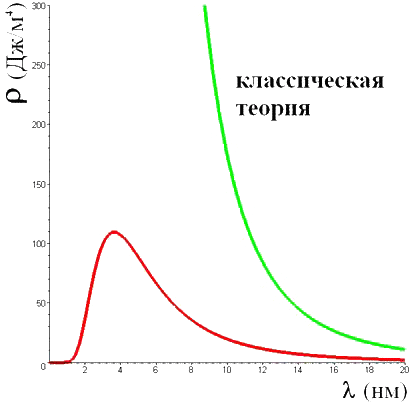
(См. рис. 9). Поскольку — плотность энергии излучения в единице объёма, приходящаяся на единичный интервал длин волн, то полная энергия равновесного теплового излучения в единице объема определяется интегралом

Но этот интеграл равен бесконечности! Таким образом, согласно классической теории энергия равновесного излучения в полости оказывается бесконечной. Это согласуется с теоремой о равномерном распределении энергии по степеням свободы, но с физической точки зрения, очевидно, абсурдно.

Подчеркнём ещё раз, что наблюдаемая в опыте картина прямо противоположна выводам классической физики: на самом деле почти вся энергия в равновесном состоянии сосредоточена внутри атомов вещества. Это противоречие называется парадоксом Больцмана.

Рис. 9. Зависимость спектральной плотности равновесного излучения от длины волны при T = 5000 K. Нижняя кривая получена экспериментально, а верхняя – теоретически по формуле классической физики (2)